shorter proof of generalized mediant inequality?

Question

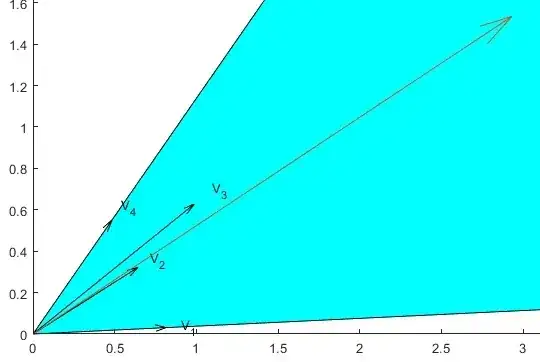
Show $\frac{a_{1}+...+a_{n}}{b_{1}+...+b_{n}}$ is between the smallest and largest fraction $\frac{a_{i}}{b_{i}}$, where $b_{i}>0$.

Attempt

Assume the largest is $\frac{a_{n}}{b_{n}}\Rightarrow$

$\frac{a_{n}}{b_{n}}-\frac{a_{1}+...+a_{n}}{b_{1}+...+b_{n}}\Rightarrow $

$\frac{b_{1}+...+b_{n-1}}{{b_{1}+...+b_{n}}}[\frac{a_{n}}{b_{n}}-\frac{a_{1}}{b_{1}+...+b_{n-1}}-...-\frac{a_{n-1}}{b_{1}+...+b_{n-1}}]\Rightarrow $

if $a_{1}<0$, $w=\frac{a_{n}}{b_{n}}-\frac{a_{1}}{b_{1}+...+b_{n-1}}-...-\frac{a_{n-1}}{b_{1}+...+b_{n-1}}>\frac{a_{n}}{b_{n}}-\frac{a_{2}}{b_{1}+...+b_{n-1}}-...-\frac{a_{n-1}}{b_{1}+...+b_{n-1}}$

any hints or solutions?

Answer 1

If you are willing to grant that the weighted average of several terms falls between the smallest term and the largest term (pretty easily shown), we can do the proof in one line.

$\frac{a_1+...+a_n}{b_1+...+b_n}$ = ($\frac{a_1}{b_1}$)($\frac{b_1}{b_1+...b_n}$) +...+($\frac{a_n}{b_n}$)($\frac{b_n}{b_1+...b_n}$) This is a weighted average of the $\frac{a_i}{b_i}$ terms and so must not be greater than the largest or smaller than the smallest.

Answer 2

We have that

$$\frac{a_n}{b_n}\ge \frac{a_i}{b_i}\iff a_nb_i\ge a_ib_n\;\;,\;\;\forall i\implies$$

$$\frac{a_n}{b_n}\ge\frac{a_1+\ldots+a_n}{b_1+\ldots+b_n}\iff a_nb_1+\ldots +a_nb_n\ge a_1b_n+\ldots+a_nb_n$$

and the claim follows from the fist part above

Now you try the other inequality.

Answer 3

Assume $$\frac{a_1}{b_1}\le\frac{a_2}{b_2}\le\dots\le\frac{a_n}{b_n}$$ and define $$N_k:=a_1+a_2+\dots+a_k\quad\text{and}\quad D_k:=b_1+b_2+\dots+b_k.$$ Using the ordinary mediant inequality, induction gives: $$\forall k\in\{2,3,\dots,n\}\quad\frac{a_1}{b_1}\le\frac{N_k}{D_k}\le\frac{a_k}{b_k}.$$ The final case $k=n$ is the claim.

Answer 4

A geometric proof without words :

But with words, it's better.

Let $V_k=\pmatrix{a_k\\b_k}$ and $\theta_k \in I$ its polar angle where $I=(0,\tfrac{\pi}{2})$

The idea is that it suffices to "transfer" the order between fractions $a_k/b_k$ considered as $\arctan(\theta_k)$ and the order of these polar angles $\theta_k$.

With more details :

As $\frac{b_k}{a_k}=\arctan{\theta_k}$, condition :

$$\frac{a_1}{b_1}<\frac{a_2}{b_2}<\ldots<\frac{a_n}{b_n}$$

plainly means that the indices of the vectors are by ascending order of the $\arctan$ of their polar angles, therefore of their polar angles (because function $\arctan$ is increasing on $I=(0,\tfrac{\pi}{2}).$)

Consider the convex cone $(C)$ (rendered with cyan color on the above figure) (see here) generated by the $V_k$s. $(C)$ has generic element $W=\sum c_k V_k$ (all $c_k>0$) which is in-between the two extremal rays $\mathbb{R_+}V_1$ and $\mathbb{R_+}V_n$.

"Being situated between" means that the polar angle of $W$ belongs to interval $(\theta_1,\theta_n).$

In our case, we are with element $W=\sum V_k=\pmatrix{a_1+a_2+\cdots+a_n\\b_1+b_2+\cdots+b_n}$ whose polar angle is in the interval $(\theta_1,\theta_n)$. Finished...