6

I've been fascinated by the idea of analytic continuation and I came across the identity theorem for holomorphic functions. (http://en.wikipedia.org/wiki/Identity_theorem)

On wikipedia it states: "Thus a holomorphic function is completely determined by its values on a (possibly quite small) neighborhood in D. This is not true for real-differentiable functions"

Is there a simple way or an accessible example to show why this is so? I'm an enthusiast with a undergraduate math background, but I have not studied complex analysis.

Jim
  • 159
  • 1
    Differentiability in $\mathbb C$ is a much, much, much stronger condition than differentiability in $\mathbb R$. – MPW Mar 19 '14 at 02:24
  • The basic reason is that every complex-differentiable function has a power series and the power series about a point defines a unique power series about every other point within its radius of convergence. – Kevin Carlson Mar 19 '14 at 02:46
  • I just thought that I'd point out that the current Purdue Problem of the Week (Number 11) is related to this idea. You should give it a shot: http://www.math.purdue.edu/pow/ – Joel Apr 02 '14 at 19:28

1 Answers1

9

Consider the function $f(x) = \mathrm{e}^{-1/x^2}$ on the reals. Although not defined at zero, it clearly has a limit at zero and that limit is zero. Now look at its derivatives: $$f'(x) = \frac{2}{x^3} f(x)$$ $$f''(x) = \frac{4-6x^2}{x^6} f(x)$$ $$f'''(x) = \frac{8-36x^2+24x^4}{x^9} f(x)$$ and so on, with the exponential overwhelming the rational function as we take limits at zero. We find, in fact, that this limiting process gives us zeroes for every derivative at zero.

Is this the zero function? No. Therefore, its power series expansion is not faithful at zero.

Why? Take a step back and look at the complex plane and notice the essential singularities pressed up against the real line at zero and discover that I "cheated" by taking limits at zero. In the reals, the limits exist, but in the complexes they do not. In short, the real line can be blind to essential features of functions. (Especially if the person posing functions to investigate is aware of this deficiency.) However, having looked at a neighborhood in the complexes, there is nothing left to know since there is nowhere for a feature to hide.

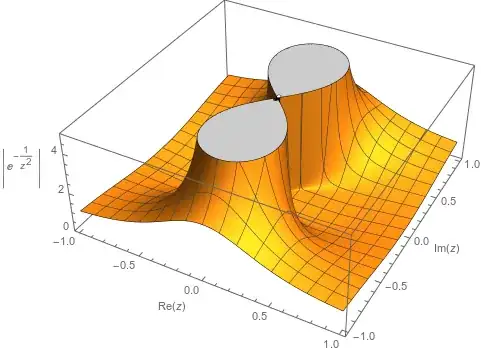
3D plot of magnitude

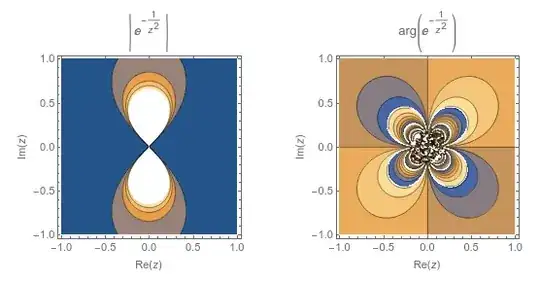
Abs/Arg plot pair

(I spent some time trying to clean up what amounts to random moire pattern in the center of the argument plot. The best I could manage follows, but is misleading about the violent flailing of the complex angle near the origin.)

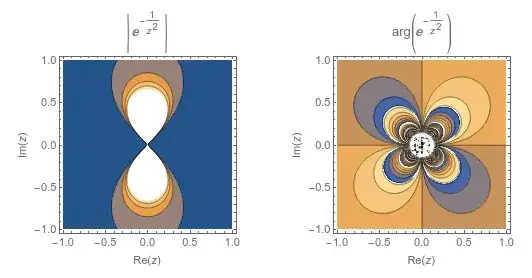
Another Abs/Arg plot pair

(What we should really be seeing is infinitely many thinner and thinner strips as we get closer to the origin. Of course, the strips are already one pixel wide in the given image -- if we attempt to thin them further, all we render is a continuous blob of contour lines.)

Eric Towers
  • 67,037