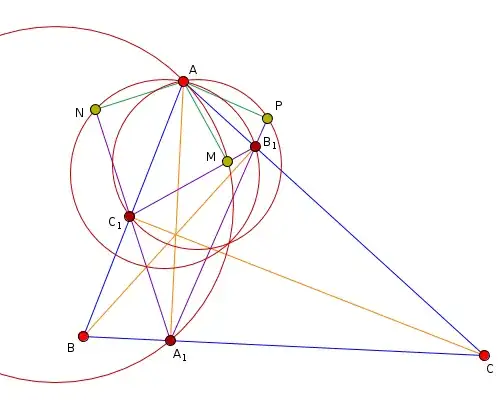
Doing the computation
Here is a coordinate-based approach, performed using Sage.
The property you want to describe is invariant under translations. You might therefore, without loss of generality, choose $A=(0,0)$. Furthermore, it is invariant under scale and rotation, so you might also choose $B=(1,0)$. So the coordinates $C=(C_x,C_y)$ can be used to parametrize all relevant cases. I'll therefore do my computations in the polynomial ring $\mathbb Q[C_x,C_y]$.
sage: PR.<Cx, Cy> = QQ[]
Now I switch to homogeneous coordinates and projective geometry. Simply append a $1$ to the coordinate vector to obtain the homogeneous coordinates of a point.
sage: A = vector(PR, [0, 0, 1])
sage: B = vector(PR, [1, 0, 1])
sage: C = vector(PR, [Cx, Cy, 1])
Then you can compute the coordinates (parameters of the normal form) of a line joining two points using the cross product. And conversely the point of intersection between two lines can be computed using the cross product as well.
sage: AB = A.cross_product(B)
sage: BC = B.cross_product(C)
sage: CA = C.cross_product(A)
Multiplying the diagonal matrix $\operatorname{diag}(1,1,0)$ with the vector of a line will give a point at infinity in the direction orthogonal to that line. Connecting that point with a finite point of your construction gives the orthogonal line passing through that point, and intersecting that with the original line gives the orthogonal projection. That's what the method orthoproj below does.
sage: IJ = diagonal_matrix([1, 1, 0])
sage: def orthoproj(point, line):
... return point.cross_product(IJ*line).cross_product(line)
sage: A1 = orthoproj(A, BC)
sage: B1 = orthoproj(B, CA)
sage: C1 = orthoproj(C, AB)
sage: AB1 = A1.cross_product(B1)
sage: BC1 = B1.cross_product(C1)
sage: CA1 = C1.cross_product(A1)
sage: M = orthoproj(A, BC1)
sage: N = orthoproj(A, CA1)
sage: P = orthoproj(A, AB1)
A circle can be described by a homogeneous equation of the form
$$\alpha(x^2+y^2)+\beta xz+\gamma yz+\delta z^2=0\;.$$
If homogeneous coordinates seem strange to you, simply imagine $z=1$ and it makes sense for normal affine coordinates as well. The parameters $\alpha,\beta,\gamma,\delta$ are only defined up to a scalar multiple. Given three points, we can obtain the parameter vector of the circle through these three points by finding any non-zero solution to the following system of equations:
$$\begin{pmatrix}
x_1^2+y_1^2 & x_1z_1 & y_1z_1 & z_1^2 \\
x_2^2+y_2^2 & x_2z_2 & y_2z_2 & z_2^2 \\
x_3^2+y_3^2 & x_3z_3 & y_3z_3 & z_3^2
\end{pmatrix}
\begin{pmatrix}\alpha\\\beta\\\gamma\\\delta\end{pmatrix}=
\begin{pmatrix}0\\0\\0\end{pmatrix}$$
One way to achieve such a solution is by computing all $3\times3$ minors of this matrix, and take them in the correct order and with alternating sings. (You can derive this idea from the $4\times4$ determinant used to check the cocircularity of four points and its computation via Laplace expansion.) While we are at it, we can also cancel common factors from these polynomials, to make things simpler. After all, multiples of the equation represent the same circle, but see below for a discussion of these factors and the special cases they encode.
sage: def squaredvec(point):
... x, y, z = point
... return vector(point.base_ring(), [x*x + y*y, x*z, y*z, z*z])
sage: def circleparam(points, cancelGCD=True):
... m = matrix(map(squaredvec, points))
... p = [(-1)^i*j for i, j in enumerate(reversed(m.minors(3)))]
... if cancelGCD:
... g = gcd(p)
... p = [i // g for i in p]
... p = vector(p)
... assert (m*p).is_zero()
... return p
sage: circles = matrix(map(circleparam,
... ((A, M, A1), (A, N, B1), (A, P, C1))))
The matrix we obtain here is this one:
$$\begin{pmatrix}
- C_x^{2} - C_y^{2} + 1 & 2 C_x^{2} + C_y^{2} - 2 C_x & C_x C_y - C_y & 0 \\
C_x^{3} + C_x C_y^{2} - C_x^{2} + C_y^{2} & - C_x^{3} - 2 C_x C_y^{2} + C_x^{2} & C_x^{2} C_y - C_x C_y & 0 \\
C_x^{2} - C_y^{2} - C_x & - C_x^{3} + C_x C_y^{2} + C_x^{2} &
-2 C_x^{2} C_y + 2 C_x C_y & 0
\end{pmatrix}$$
The rows of this matrix are the circle parameters of your three circles. It is no surprise that the $\delta$ parameter of all three circles is zero. After all, since point $A$ lies on each of them, the coefficient of $z^2$ has to be zero. Now all that remains to check is that this matrix doesn't have full rank. Seeing the above structure, you could simply check the determinant of the left $3\times 3$ block. But if you hadn't looked at the matrix first, you might prefer to check all $3\times3$ minors:
sage: all(minor.is_zero() for minor in circles.minors(3))
True
This tells you that the third circle is always a linear combination of the first two circles (except in the special case when the first two circles are equal). A circle which is a linear combination of two other circles has all the points of intersection in common with these. So now you know that all three circles must pass through two common points, $A$ and that other one.
In case you are not convinced, I can give the homogeneous coordinates of the second common point explicitly:
$$Q=\begin{pmatrix}
6 C_x^2 C_y^2 + 3 C_x C_y^2 \\
-3 C_x^3 C_y + 3 C_x C_y^3 + 3 C_x^2 C_y \\
C_x^4 + 2 C_x^2 C_y^2 + C_y^4 - 2 C_x^3 + 6 C_x C_y^2 + C_x^2 + C_y^2
\end{pmatrix}$$
Special cases
Indicated by Blue
In a comment, Blue pointed out several special cases. Let's look at these:
When there's a right angle at $B$ or $C$, the three circles coincide, so there's not a unique "second point" (other than $A$) on them.
A right angle at $B$ would mean $C_x=1$. In that case, the matrix above would have rank $1$, which corresponds to three circles coinciding:
$$\begin{pmatrix}
- C_y^{2} & C_y^{2} & 0 & 0 \\
2 C_y^{2} & -2 C_y^{2} & 0 & 0 \\
- C_y^{2} & C_y^{2} & 0 & 0
\end{pmatrix}$$
For the case of a right angle at $C$, you could simply exchange the roles of $B$ and $C$. Or you could choose a rational representation of $C$ on the Thales' circle over $AB$. Choosing $$C=\left(\frac{t^2}{t^2+1},\frac{t}{t^2+1}\right)$$ satisfies $C_x^2+C_y^2-C_x=0$, so it will result in a right angle. The resulting circle parameter matrix will be
\begin{align*}
\frac1{\bigl(t^2 + 1\bigr)^3}&\begin{pmatrix}
t^{4} + 2 t^{2} + 1 & -t^{4} - t^{2} & -t^{3} - t & 0 \\
t^{4} + t^{2} & -t^{4} & -t^{3} & 0 \\
-2 t^{4} - 2 t^{2} & 2 t^{4} & 2 t^{3} & 0
\end{pmatrix}=\\
\frac1{\bigl(t^2 + 1\bigr)^3}&
\begin{pmatrix}t^2+1\\t^2\\-2t^2\end{pmatrix}\cdot
(t^2+1\quad -t^2\quad -t\quad 0)
\end{align*}
which has rank $1$ as well, as evidenced by the factorization printed above.
Note however that the coinciding circles Blue mentioned only occur as the limiting case in a continuous movement towards this special situation. If constructed directly in this situations, one of the lines joining the feet of two heights will be undefined since its defining points coincide at the right angle.
When there's a right angle at $A$, two of the circles become point-circles at $A$, so there's no "second point" at all.
This is the case for $C_x=0$. In that case, the marix would become
$$\begin{pmatrix}
- C_y^{2} + 1 & C_y^{2} & - C_y & 0 \\
C_y^{2} & 0 & 0 & 0 \\
- C_y^{2} & 0 & 0 & 0
\end{pmatrix}$$
which has rank $2$, but the second and third row are degenerate. They represent the equation $x^2+y^2=0$, which can be interpreted as a circle of radius zero, centred at the origin. These are the “point-circles” Blue was referring to.
Like in the previous case, a straight construction with a right angle at $A$ leads to an undefined situation, since $B_1=C_1=A$, so the line $B_1C_1$ and therefore the point $M$ is not defined. The point-circles only occur as the limit case if you move the points continuously towards this degenerate situation.
Reading them from the cancelled factors
In all these cases where intermediate results are undefined, the corresponding rows of the parameter matrix would more appropriately be all zeros. This does not happen in the above formulation due to the fact that we cancelled common factors, thus removing some singularities. For example, $C_x$ is such a common factor, and by dividing the whole row by that factor, we eliminated zero rows for the case of $C_x=0$.
In case you wonder about what these common factors were which we cancelled, and what other strange situations we might have missed because of them, here they are:
\begin{alignat*}{5}
& C_y^3
&&\cdot\, C_x^5
&&\cdot\, (C_x^2 + C_y^2)
&&\cdot\, (C_x^2 + C_y^2 - 2 C_x + 1)^2
\\
& C_y
&&\cdot\, C_x^2
&&\cdot\, (C_x^2 + C_y^2)^2
&&\cdot\, (C_x^2 + C_y^2 - 2 C_x + 1)
&&\cdot\, (C_x - 1)^4
\\
& C_y
&&\cdot\, C_x^2
&&\cdot\, (C_x^2 + C_y^2)
&&\cdot\, (C_x^2 + C_y^2 - 2 C_x + 1)
&&\cdot\, (C_x^2 + C_y^2 - C_x)^4
\end{alignat*}
As you can see, $C_y$ is a factor in each of them, representing the case of a degenerate triangle $ABC$ where all corners are collinear. $C_x$ is the factor corresponding to a right angle at $A$ as discussed above. $(C_x-1)$ is a factor in one row as well, and so is $(C_x^2 + C_y^2 - C_x)$, so all the special cases discussed above would lead to at least one all-zero row if we hadn't cancelled these factors. That term $(C_x^2 + C_y^2)$ corresponds to the case $A=C$, which is obviously degenerate as well. In a similar way, $(C_x^2 + C_y^2 - 2 C_x + 1)=\bigl((C_x-1)^2+C_y^2\bigr)$ represents the degenerate case $B=C$. The third case of $A=B$ was avoided by our choice of coordinates.
So perhaps it is best to say that the above proof works for points $A,B,C$ “in general position”, and to give a list of non-degeneracy assumptions if such is required. In most cases, it should not be required. But excluding three collinear corners as well as right angles should be enough.