I plotted the function
$$f(x) = \sum_{n=1}^x \frac{1}{n}$$
in Wolfram Alpha over $x\in\mathbb{R}$ and it gave me some unexpected behavior for negative $x$. This function is obvious for $x\in\mathbb{N}$. Can anyone explain how Wolfram Alpha is computing this? Is the plot below a numerical artifact or is there some function on $x\in\mathbb{R}$ that agrees with $f(x)$ when $x\in\mathbb{N}$?
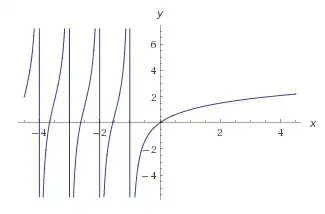
https://www.wolframalpha.com/input/?i=plot+sum+1%2Fn+n%3D1+to+x