3

I know a proof of this statement, see How to demonstrate that there is no all-prime generating polynomial with rational cofficents?

My question is that, in the book 

Introduction to Modern Number Theory - Fundamental Problems, Ideas and Theories

by Manin, Yu. I., Panchishkin, Alexei A,

it says (p16)

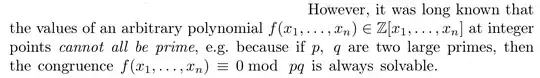
enter image description here

I would like to know if this is correct. If I understand it correctly, then $x^2+1$ is a counterexample of this, by considering the Legendre symbol $(\frac{-1}{p}) = (-1)^{\frac{p-1}{2}}$.

Community
  • 1
user565739
  • 279
  • 3
    You're right, as far as I can tell. I think one needs to first assume that $f(\vec x)\equiv 0\pmod p$ and $f(\vec x)\equiv 0\pmod q$ are individually solvable. – Greg Martin Mar 27 '14 at 22:17

1 Answers1

-1

suppose the polynomial P(x) takes prime value for each integer k.assume r is a root of P(x).so P(r)=0

  • now k -r|P(k) -P(r)$ \Rightarrow $k -r|P(k)=m=a prime. so clearly k -r=m or 1
  • so clearly k-n=a prime or 1 for all roots n of P(x)
  • consider P(x)=a(x-r)(x-c)(x-d)....................(x-v)[r,c,d,.........,v are roots]
  • now P(k)=a(k-r)(k-c)(k-d)................(k-v)=a(a prime or 1)(a prime or1)....................(a prime or 1)=a constant
  • but P(x) is non constant.so a contradiction!!!!!!
krishan acton
  • 639