If you assume that your group is generated by your elements $x$ and $y$, so if you just look at the subgroup $\langle x, y\rangle$, then you can work out some stuff. The following answer looks at the "maximal possible" examples, with respect to homomorphic images.
Short version: It depends on the following sum. $$\frac{1}{|x|}+\frac{1}{|y|}+\frac{1}{|xy|}$$ If this is greater than one then your group is finite, while if it is less than or equal to one then your group is infinite. If it is less than one then your group is hyperbolic, so you get lots of things happening and lots of things not happening (but such things are not necessarily preserved under homomorphic images).
Long version:
A triangle group is a group with a presentation of the following form.
$$T_{(i, j, k)}=\langle a, b; a^i, b^j, (ab)^k\rangle\cong \langle a, b, c; a^i, b^j, c^k, abc\rangle$$
These groups are non-trivial for $i, j, k>1$. They are called triangle groups because they correspond to the symmetries$^{[1]}$ of a plane tiled with congruent triangles with angles $\frac{\pi}{i}$, $\frac{\pi}{j}$ and $\frac{\pi}{k}$ (so they act non-trivially on some object, so cannot be trivial).
Therefore, for each pair triple $(i, j, k)$ there exists a group with elements $x$ and $y$ of order $i$ and $j$ respectively such that $xy$ has order $k$. Note that taking the free product $C_i\ast C_j$ we see that $k$ can be infinite also.
You might wonder if the group $T_{(i, j, k)}$ corresponding to your favourite triple is finite or infinite, and I will mention that, below.
For example, the $(3, 3, 3)$ triangle group corresponds to the tiling of the Euclidean plane by equilateral triangles, which is illustrated below.

Triangle groups act on their corresponding tilings as follows.
- Fix a triangle and label the vertices $A$, $B$ and $C$.
- The generator $a$ rotates the tiling around the vertex $A$.
- Similarly for $b$ and $c$.
Using this action, it is not difficult to prove that in each triangle group $\langle a, b, c; a^i, b^j, c^k, abc\rangle$ the subgroups $\langle a\rangle$, $\langle b\rangle$ and $\langle c\rangle$ intersect trivially.
Now, the above example $T_{(3, 3, 3)}$ is infinite because the tiling is infinite. In general, the following hold.
- If $\frac1i+\frac1j+\frac1k<1$ then the tiling is a tiling of the hyperbolic plane (an infinite plane) and so the group is infinite. Such groups are hyperbolic (see here), so, for example, they are not soluble and do note contain $\mathbb{Z}\times\mathbb{Z}$. For example, the triple $(3,3,4)$ corresponds to the following tiling.

- If $\frac1i+\frac1j+\frac1k=1$ then the tiling is a tiling of the Euclidean plane (an infinite plane) and so the group is infinite. There are only finitely many such triples $(i, j, k)$ and so there are only finitely many such tilings of the Euclidean plane, and only finitely many Euclidean triangle groups.
- If $\frac1i+\frac1j+\frac1k>1$ then the tiling is a tiling of a sphere (a finite object) and so the group is finite. For example, the Klein 4-group acts on the following tiling of the sphere.
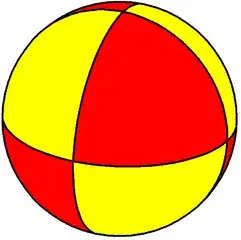
For more details and examples, please see the wikipedia article$^{[2]}$. Note: This is also where I stole the above images from.
$^{[1]}$ Translations and rotations, but not reflections. If you include reflections the groups I am discussing form an index-two subgroup.
$^{[2]}$ What the article calls triangle groups is actually the complete group of symmetries of the tiling, including reflections. This is, in my opinion, non-standard (I have written a bit, and read a lot, on triangle groups). What I call triangle groups the article calls "von Dyke groups".


