Cantor's Teepee is Totally Disconnected

Question

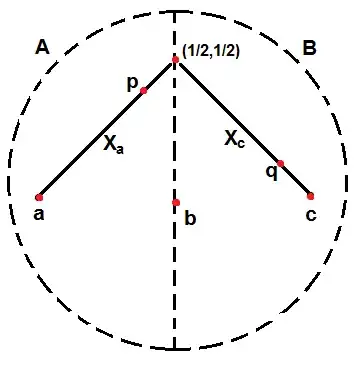
Let $C^\prime$ be the Cantor set and let $C = C^\prime \times \{0\}$ (viewed as a subset of $\mathbb{R}^2$). For $c \in C$, let $L(c)$ denote the half-closed line segment connecting $(c,0)$ to $(\tfrac{1}{2}, \tfrac{1}{2})$ (including $(c,0)$ but excluding $(\tfrac{1}{2}, \tfrac{1}{2})$).

If $c \in C$ is $(0,0)$, $(1,0)$, or an endpoint of an interval deleted in the Cantor set, let $X_{c} = \{ (x,y) \in L(c) : y \in \mathbb{Q} \}$. For all other $c \in C$, let $X_{c} = \{ (x,y) \in L(c) : y \notin \mathbb{Q} \}$.

Cantor's Teepee is the set $\bigcup_{c \in C} X_{c}$ equipped with the subspace topology inherited from the standard topology on $\mathbb{R}^2$.

I've found several references to the fact that Cantor's Teepee is totally disconnected, but I cannot quite prove it.

---

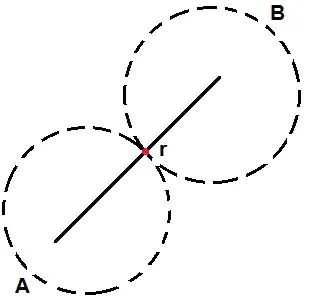
It was brought to my attention in the comments that I had taken the wrong definition for totally disconnected when first working on this problem, as demonstrated in the following example. The property I had been attempting to prove was totally separated, which lead to the quandary I was experiencing below.

In particular, I cannot seem to separate two points that belong to the same $X_c$. For concreteness:

What are two separated open sets $A$ and $B$ such that

<ul>
<li>$A$ and $B$ witness the disconnectedness of Cantor's Teepee,</li>
<li>$(0,0) \in A$, and</li>
<li>$(\tfrac{1}{4}, \tfrac{1}{4}) \in B$?</li>
</ul>

Notice $(0,0), (\tfrac{1}{4}, \tfrac{1}{4}) \in X_0$. Presumably the method that works for this example can be easily modified to work for any pair of points belonging to the same $X_c$.

Answer 1

Let $T$ be the Cantor teepee. Every point $t\in T$ lies on unique interval of the form $[c, (1/2, 1/2)]$, where $c\in C'$. The map $f: t\mapsto c$ is continuous on $T$. Suppose $A\subset T$ is a connected subset. Then $f(A)$ is also connected. Since $C'$ is totally disconnected, $f(A)$ is a single point. Thus, $A$ is contained in subset $L_c$. But each $L_c$ is clearly totally disconnected. Hence, $A$ is a single point. Thus, $T$ is totally disconnected. qed

Answer 2

The following proof is a clunkier version of that given by studiosus, but I provide some details that I think will be helpful for my students who are involved with this problem.

---

Let $Y$ be any subset of Cantor's Teepee containing more than one point. Our goal is to produce two sets $A$ and $B$ such that

• $A$ and $B$ are separated open sets in the subspace topology induced by $Y$ and
• $Y = A \cup B$.

Since Cantor's Teepee is itself a subspace of the usual topology on $\mathbb{R}^2$, we may revise these conditions to read

• $A$ and $B$ are separated open sets in the usual topology on $\mathbb{R}$ and
• $Y \subseteq A \cup B$.

Now, suppose $Y$ contains points $p \in X_a$ and $q \in X_c$ with $a \neq c$ (that is, $Y$ witnesses more than one "strand" of the teepee). Choose any real number $b$ such that $a < b < c$ and $b$ lies in a deleted interval of the Cantor set. To obtain the separated open sets $A$ and $B$, take any open set containing $Y$ (or even the entire teepee) and "split" it along the line connecting $(b,0)$ and $(1/2,1/2)$ (see figure).

Suppose instead that all points of $Y$ belong to a single strand. The $y$-coordinates of points belonging to this strand are either all rational or all irrational. In either case, we can easily separate the strand by passing our open sets through a point $r$ with $y$-coordinate of the opposite type (see figure).

Therefore every subset of Cantor's teepee with more than one point is disconnected, which is to say Cantor's teepee is totally disconnected.