What is a sufficient condition for the limit to be differentiable?
Certainly pointwise convergence of derivatives is not enough:
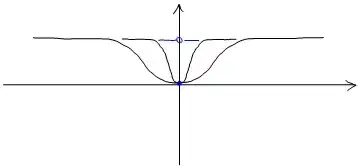
Also uniform convergence is not enough:
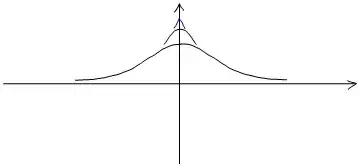
Even both together is not enough!
(See second example!)
What is a sufficient condition for the limit to be differentiable?
Certainly pointwise convergence of derivatives is not enough:

Also uniform convergence is not enough:

Even both together is not enough!
(See second example!)
The derivatives have to converge uniformly and the original functions have to converge in some point $x_0$. So if you got some sequence $f_n$ then each $f_n$ must be differentiable and $f_n' \to g$ uniformly for some $g$. If $f_n(x_0)$ converges for some $x_0$, $f_n\to f$ uniformly for some differentiable $f$ and $f′=g$.
Proof:
(I) Let $x \in [a,b]$. We show that $(f_n(x))_{n=1}^\infty$ is Cauchy.
Let $\epsilon > 0$. Since $f_n' \to g$ uniformly we can find $N$ with $|f_n'(y)-f_m'(y)| < \epsilon$ if $n,m \geq N$ and $y \in [a,b]$. Let $n,m \geq N$. Applying the Mean Value Theorem to $f_n-f_m$ we find a $\xi \in [a,b]$ with $$ |(f_n(x)-f_m(x))-(f_n(x_0)-f_m(x_0))| < |(f_n-f_m)'(\xi)||x-x_0| < \epsilon |x-x_0|. $$ By the above we get \begin{align*} |f_n(x)-f_m(x)| & \leq |(f_n(x)-f_m(x))-(f_n(x_0)-f_m(x_0))| + |f_n(x_0)-f_m(x_0)|\\ & \leq \epsilon (b-a) +\epsilon. \end{align*} if $n,m$ large enough.
(II) We now may define $f(x) := \lim_n f_n(x)$ for $x \in [a,b]$. We further see that $$ \forall x: |f_n(x)-f_m(x)| < \epsilon $$ if $n,m$ large enough. Taking the limit in $m \to \infty$ we get $$ \forall x: |f_n(x)-f(x)| < \epsilon $$ for sufficiently large $n$. That is $f_n \to f$ uniformly.
(III) We now show that $f' =g$. Let $x \in [a,b]$ and $\epsilon > 0$ and $y \neq x$. We want to show that $$ \left | \frac{f(x)-f(y)}{x-y} - g(x) \right | <\epsilon $$ if $y$ is close to $x$. We do the following: \begin{align*} \left | \frac{f(x)-f(y)}{x-y} - g(x) \right | \\ \leq \left | \frac{f(x)-f(y)}{x-y} - \frac{f_n(x)-f_n(y)}{x-y} \right | + \left | \frac{f_n(x)-f_n(y)}{x-y} - g(x) \right | \\ \leq \underbrace{\left | \frac{f(x)-f(y)}{x-y} - \frac{f_n(x)-f_n(y)}{x-y} \right |}_{(\alpha)} + \underbrace{\left | \frac{f_n(x)-f_n(y)}{x-y} - f_n'(x) \right |}_{(\beta)}+ \underbrace{\left | f_n'(x) - g(x) \right|}_{(\gamma)} \end{align*}
(IV) We now check how we must choose $n$ and the neighborhood around $x$ to get the foregoing expression small. We first consider $(\alpha)$. We get $$ (\alpha) = \lim_{m \to \infty} \left | \frac{f_m(x)-f_m(y)}{x-y} - \frac{f_n(x)-f_n(y)}{x-y} \right | $$ As we did in (I) we can find a $N$ s.t. $$ \left | \frac{f_m(x)-f_m(y)}{x-y} - \frac{f_n(x)-f_n(y)}{x-y} \right | < \epsilon (b-a) $$ if $n \geq N$. This inequality holds for all $x,y$. So independent of $x$ and $y$ we get $(\alpha) < \epsilon (b-a)$ if $n \geq N$.
Sine $f_n' \to g$ uniformly we can find a $N'$ with $n \geq N' \Rightarrow |f_n'(x)-g(x)| < \epsilon$. Take $K := \max(N,N')$ and let $n := K$.
Then $f_n$ is differentiable at $x$ and if $y$ is close to $x$ we get $(\beta) < \epsilon$. So $(\beta)$ determindes how close $y$ must be to $x$.
This proves the claim.
(V) Note that we first consider some inequality which holds for all $y$ and $n$. Then we find some $n = K$ which makes $(\alpha)$ and $(\gamma)$ small for all $y$. By choosing $y$ close to $x$ we also make $(\beta)$ small to get the desired result. $\blacksquare$