Evaluate $\int_0^\infty \frac{(\ln x)^2}{x^2+4} \ dx$ using complex analysis.

Question

Evaluate $\int_0^\infty \frac{(\ln x)^2}{x^2+4} \ dx$. This is the last question in our review for complex analysis. Hints were available upon request, but being the student I am, I waited until the last minute to do this. Can anyone give a detailed answer? It would greatly appreciated. This is part of our residue theorem review, which is how we were taught to evaluate such integrals.

Answer 1

Consider the contour integral

$$\oint_C dz \frac{\log^3{z}}{z^2+4} $$

where $C$ is a keyhole contour about the positive real axis, with outer radius $R$ and inner radius $\epsilon$. The contour integral is then equal to

$$\int_{\epsilon}^R dx \frac{\log^3{x}}{x^2+4} +i R \int_0^{2 \pi} d\theta \, e^{i \theta} \frac{\log^3{(R e^{i \theta})}}{R^2 e^{i 2 \theta}+4} \\ + \int_R^{\epsilon} dx \, \frac{(\log{x}+i 2 \pi)^3}{x^2+4} + i \epsilon \int_{2 \pi}^0 d\phi \, e^{i \phi} \frac{\log^3{(\epsilon e^{i \phi})}}{\epsilon^2 e^{i 2 \phi}+4}$$

As $R \to \infty$ the second integral vanishes as $2 \pi R \log^3{R}/(R^2-4)$; as $\epsilon \to 0$, the fourth integral vanishes as $(\pi/2) \epsilon \log^3{\epsilon}$. In this limit, then, the contour integral is

$$-i 6 \pi\int_0^{\infty} dx \frac{\log^2{x}}{x^2+4} + 12 \pi^2 \int_0^{\infty} dx \frac{\log{x}}{x^2+4} + i 8 \pi^3 \int_0^{\infty} \frac{dx}{x^2+4}$$

The third integral is familiar, and is equal to $i 8 \pi^3 (\pi/4) = i 2 \pi^4$. The second integral is evaluated in a similar manner:

$$\begin{align}\int_0^{\infty} dx \frac{\log^2{x}-(\log{x}+i 2 \pi)^2}{x^2+4} &= -i 4 \pi\int_0^{\infty} dx \frac{\log{x}}{x^2+4} + 4 \pi^2 \int_0^{\infty} \frac{dx}{x^2+4} \\ &=-i 4 \pi\int_0^{\infty} dx \frac{\log{x}}{x^2+4} +\pi^3 \\ &= \underbrace{i 2 \pi \frac14 \left ( -i (\log{2}+i \frac{\pi}{2})^2+ i (\log{2}+i \frac{3\pi}{2})^2\right )}_{\text{residue theorem}}\\ &= i \pi (-\pi \log{2} - i \pi^2)\\ &= \pi^3 - i \pi^2 \log{2}\end{align}$$

so that

$$\int_0^{\infty} dx \frac{\log{x}}{x^2+4} = \frac{\pi}{4} \log{2}$$

Therefore, by the residue theorem,

$$\begin{align}-i 6 \pi\int_0^{\infty} dx \frac{\log^2{x}}{x^2+4} + 3 \pi^3 \log{2} + i 2 \pi^4 &= i 2 \pi \frac14 \left ( -i (\log{2}+i \frac{\pi}{2})^3+ i (\log{2}+i \frac{3\pi}{2})^3\right ) \\ &= 3 \pi^3 \log{2} + i \left (\frac{13 \pi^4}{8}-\frac{3 \pi^2}{2} \log^2{2} \right ) \end{align} $$

Therefore

$$\int_0^{\infty} dx \frac{\log^2{x}}{x^2+4} = \frac{\pi^3}{16} + \frac{\pi}{4} \log^2{2} $$

Answer 2

I'm going to post a slightly different approach using contour integration.

Consider $ \displaystyle f(z) = \frac{\log^{2}(z)}{z^{2}+4}$ where the branch cut for $\log z$ is placed along the negative imaginary axis.

Now integrate around a contour that consists of the line segment $[-R,R]$ (with a half-circle indentation of radius $r$ around the branch point at the origin) and the upper half of the circle $|z|=R$.

Letting $ r \to 0$ and $R \to \infty$, the integral vanishes along both half-circles.

So we have

$$\int_{0}^{\infty} \frac{\log^{2} (x)}{x^{2}+4} \ dx + \int_{-\infty}^{0} \frac{(\log |x|+ i \pi)^{2}}{x^{2}+4} \ dx = 2 \pi i \ \text{Res}[f(z),2i].$$

And equating the imaginary parts on both sides of the equation,

$$ \begin{align}2 \int_{0}^{\infty} \frac{\log^{2} (x)}{x^{2}+4} \ dx - \pi^{2} \int_{0}^{\infty} \frac{1}{x^{2}+4} \ dx &= \text{Re} \ 2 \pi i \ \text{Res}[f(z),2i] \\ &= 2 \pi \ \text{Re} \ i \lim_{z \to 2i} \frac{\log^{2} (z)}{z+2i} \\ &= 2 \pi \ \text{Re} \ i \frac{(\log 2 + \frac{i \pi}{2})^{2}}{4i} \\ &=\frac{\pi}{2} \log^{2}(2) - \frac{\pi^{3}}{8}. \end{align}$$

But

$$ \int_{0}^{\infty} \frac{1}{x^{2}+4} \ dx = \frac{1}{2} \arctan (\frac{x}{2}) \Big|^{\infty}_{0} = \frac{\pi}{4}.$$

Therefore,

$$ \int_{0}^{\infty} \frac{\log^{2} (x)}{x^{2}+4} \ dx = \frac{\pi}{4} \log^{2}(2) + \frac{\pi^{3}}{16}.$$

Answer 3

Here is a method without complex analysis. Setting $x=2t$, we get $$I = \int_0^{\infty} \dfrac{\ln^2(2t)}{4(t^2+1)}2dt \implies 2I = \int_0^{\infty}\dfrac{\ln^2(2)}{1+t^2}dt + 2\ln(2)\int_0^{\infty}\dfrac{\ln(t)}{1+t^2}dt + \int_0^{\infty}\dfrac{\ln^2(t)}{1+t^2}dt$$ $$\int_0^{\infty}\dfrac{\ln^2(2)}{1+t^2}dt = \dfrac{\pi \ln^2(2)}2$$ $$\int_0^{\infty}\dfrac{\ln(t)}{1+t^2}dt = \int_0^1\dfrac{\ln(t)}{1+t^2}dt + \int_1^{\infty}\dfrac{\ln(t)}{1+t^2}dt = \int_0^1\dfrac{\ln(t)}{1+t^2}dt + \int_1^{0}\dfrac{-\ln(t)}{1+1/t^2}\dfrac{-dt}{t^2} = 0$$ \begin{align} \int_0^{\infty}\dfrac{\ln^2(t)}{1+t^2}dt & = \int_0^1\dfrac{\ln^2(t)}{1+t^2}dt + \int_1^{\infty}\dfrac{\ln^2(t)}{1+t^2}dt = \int_0^1\dfrac{\ln^2(t)}{1+t^2}dt + \int_1^{0}\dfrac{\ln^2(t)}{1+1/t^2}\dfrac{-dt}{t^2}\\ & = 2\int_0^1\dfrac{\ln^2(t)}{1+t^2}dt = 2 \sum_{k=0}^{\infty}(-1)^k \int_0^1 t^{2k} \ln^2(t)dt = 4 \sum_{k=0}^{\infty} \dfrac{(-1)^{k}}{(2k+1)^3} = \dfrac{\pi^3}8 \end{align} Hence, the answer is $$\boxed{I = \dfrac{\pi \ln^2(2)}4 + \dfrac{\pi^3}{16}}$$

Answer 4

$\newcommand{\+}{^{\dagger}} \newcommand{\angles}[1]{\left\langle\, #1 \,\right\rangle} \newcommand{\braces}[1]{\left\lbrace\, #1 \,\right\rbrace} \newcommand{\bracks}[1]{\left\lbrack\, #1 \,\right\rbrack} \newcommand{\ceil}[1]{\,\left\lceil\, #1 \,\right\rceil\,} \newcommand{\dd}{{\rm d}} \newcommand{\down}{\downarrow} \newcommand{\ds}[1]{\displaystyle{#1}} \newcommand{\expo}[1]{\,{\rm e}^{#1}\,} \newcommand{\fermi}{\,{\rm f}} \newcommand{\floor}[1]{\,\left\lfloor #1 \right\rfloor\,} \newcommand{\half}{{1 \over 2}} \newcommand{\ic}{{\rm i}} \newcommand{\iff}{\Longleftrightarrow} \newcommand{\imp}{\Longrightarrow} \newcommand{\isdiv}{\,\left.\right\vert\,} \newcommand{\ket}[1]{\left\vert #1\right\rangle} \newcommand{\ol}[1]{\overline{#1}} \newcommand{\pars}[1]{\left(\, #1 \,\right)} \newcommand{\partiald}[3][]{\frac{\partial^{#1} #2}{\partial #3^{#1}}} \newcommand{\pp}{{\cal P}} \newcommand{\root}[2][]{\,\sqrt[#1]{\vphantom{\large A}\,#2\,}\,} \newcommand{\sech}{\,{\rm sech}} \newcommand{\sgn}{\,{\rm sgn}} \newcommand{\totald}[3][]{\frac{{\rm d}^{#1} #2}{{\rm d} #3^{#1}}} \newcommand{\ul}[1]{\underline{#1}} \newcommand{\verts}[1]{\left\vert\, #1 \,\right\vert} \newcommand{\wt}[1]{\widetilde{#1}}$ $\ds{\int_{0}^{\infty}{\ln^{2}\pars{x} \over x^{2} + 4}\,\dd x:\ {\large ?}}$.

\begin{align}&\color{#c00000}{\int_{0}^{\infty} {\ln^{2}\pars{x} \over x^{2} + 4}\,\dd x} =\int_{0}^{\infty}{\ln^{2}\pars{x^{1/2}} \over x + 4}\,\half\,x^{-1/2}\,\dd x ={1 \over 8}\int_{0}^{\infty}{x^{-1/2}\ln^{2}\pars{x} \over x + 4}\,\dd x \\[3mm]&={1 \over 8}\lim_{\mu \to -1/2}\partiald[2]{}{\mu} \color{#00f}{\int_{0}^{\infty}{x^{\mu} \over x + 4}\,\dd x}\tag{1} \end{align}

With the following contour, the integral is easily evaluated:

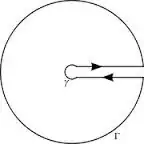\begin{align}&\color{#00f}{\int_{0}^{\infty}{x^{\mu} \over x + 4}\,\dd x} =2\pi\ic\pars{4^{\mu}\expo{\ic\pi\mu}} -\int_{\infty}^{0}{x^{\mu}\expo{2\pi\ic\mu} \over x + 4}\,\dd x \end{align}

$$ \color{#00f}{\int_{0}^{\infty}{x^{\mu} \over x + 4}\,\dd x} =2\pi\ic\,{4^{\mu}\expo{\ic\pi\mu} \over 1 - \expo{2\pi\ic\mu}} =-\pi\,{4^{\mu} \over \sin\pars{\pi\mu}} $$

\begin{align}& \partiald[2]{}{\mu}\color{#00f}{\int_{0}^{\infty}{x^{\mu} \over x + 4}\,\dd x} \\[3mm]&=-2^{2m}\,\pi\,\csc\pars{\pi \mu}\braces{\vphantom{\LARGE A} \pi^2\bracks{\vphantom{\Large A}2\csc^{2}\pars{\pi\mu} - 1} -4\pi\ln\pars{2}\cot\pars{\pi\mu} + 4\ln^{2}\pars{2}} \end{align}

\begin{align}&\lim_{\mu \to -1/2} \partiald[2]{}{\mu}\color{#00f}{\int_{0}^{\infty}{x^{\mu} \over x + 4}\,\dd x} =\half\,\pi^{3} + 2\pi\ln^{2}\pars{2} \end{align}

Replacing in $\pars{1}$: $$\color{#66f}{\large\int_{0}^{\infty} {\ln^{2}\pars{x} \over x^{2} + 4}\,\dd x} = \color{#66f}{\large{1 \over 16}\,\pi^{3} + {1 \over 4}\,\pi\ln^{2}\pars{2}} \approx 2.3152 $$