This is a snippet from my book.
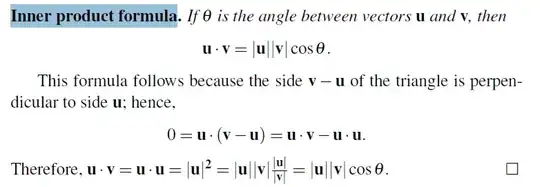
How did they get from $|{\bf u}|^2={\bf u}\cdot{\bf v}=|{\bf u}||{\bf v}|\frac{|{\bf u}|}{|{\bf v}|}$?
This is a snippet from my book.
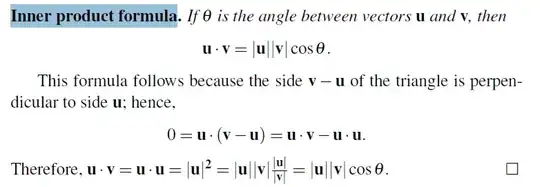
How did they get from $|{\bf u}|^2={\bf u}\cdot{\bf v}=|{\bf u}||{\bf v}|\frac{|{\bf u}|}{|{\bf v}|}$?
Well, $$|\vec{u}|^2=|\vec{u}|^2\frac{|\vec{v}|}{|\vec{v}|}=|\vec{u}||\vec{v}|\frac{|\vec{u}|}{|\vec{v}|}= |\vec{u}||\vec{v}|\text{cos}(\theta)\,\,,$$ since $|\vec{v}|/|\vec{v}|=1$.
I dont understand the comments from your book, but I assume the question is how to prove the equivalence of the two definitions of dot product, $\mathbf{u}\cdot \mathbf{v}=u_1v_1+u_2v_2+u_3 v_3$, and the equation $\mathbf{u}\cdot \mathbf{v}=|\mathbf{u}||\mathbf{v}| \cos \theta$. This is a consequence of the cosine law, if we take the triangle with sides $\mathbf{u},\mathbf{v}$ and $\mathbf{u}-\mathbf{v}$ then the cosine law reads $$|\mathbf{u}-\mathbf{v}|^2=|\mathbf{u}|^2+|\mathbf{v}|^2-2|\mathbf{u}||\mathbf{v}|\cos \theta$$ using $$|\mathbf{u}-\mathbf{v}|^2==|\mathbf{u}|^2+|\mathbf{v}|^2 -2\mathbf{u}\cdot \mathbf{v}$$ we get the desired result.
Under regular Euclidean geometry, the distance between two points $a=(x_1,y_1)$ and $b=(x_2,y_2)$ is defined as $$d(a,b)=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}.$$ Given a vector $\textbf{u}=(u_1,u_2,u_3)$, we know that $\textbf{u}=\sqrt{u_1^2+u_2^2+u_3^2}$. So from our definition of distance, we see that $\textbf{u}$ indicates the distance from the origin $(0,0,0)$ to $(a,b,c)$, or $\textbf{u}=d((0,0,0),\textbf{u})$. This relationship may help with the following explanation.
Using the regular notion of a dot product (i.e. $\textbf{u}\cdot\textbf{u}=u_1^2+u_2^2+u_3^2$), it is easy to check that $\textbf{||u||}^2=\textbf{u}\cdot\textbf{u}$ (see above). So from $0=\textbf{u}\cdot\textbf{v}-\textbf{u}\cdot\textbf{u}$, we have $\textbf{u}\cdot\textbf{v} =\textbf{u}\cdot\textbf{u}=\textbf{||u||}^2$. From there we multiply $\textbf{||u||}^2$ by $\frac{ \textbf{||v||}}{\textbf{||v||}}$. Finally, noticing that $\frac{\textbf{||u||}}{\textbf{||v||}} = cos\theta$, we have $$\textbf{u}\cdot\textbf{v}=||\textbf{u}||*||\textbf{v}||cos\theta.$$
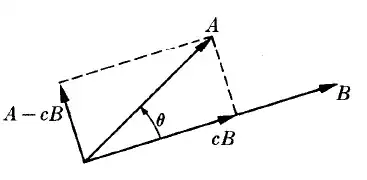
$\textbf{A really nice construction of this proof}$: Let $\textbf{A,B}$ be two vectors and $B$ $\neq O$. We seek a vector $P$ such that, $$(\textbf{A} -P) \cdot \textbf{B} = 0$$ and $P=c\textbf{B}$ for some number $c$. Suppose we can find such a number $c$, namely one satisfying, $$(A-cB) \cdot B = 0$$ We then get $$\textbf{A} \cdot \textbf{B} = c\textbf{B} \cdot \textbf{B}$$ and therefore $c=\frac{ \textbf{A} \cdot \textbf{B}}{\textbf{B} \cdot \textbf{B}}$. From this construction and use of what we know about planee geometry, $$\cos(\theta) = \frac{c||\textbf{B}||}{||\textbf{A}||}$$ and substituting in our value for $c$ we get, $$A \cdot B = ||\textbf{A}|| ||\textbf{B}|| \cos(\theta)$$ \
$\textbf{Picture for our Construction}$