Question about the proof of Harnack's inequality in Evans and Gilbarg's PDE book

Question

I have some trouble in understanding the proof of Harnack's inequality. Since I have consulted two books, I explained my three questions one by one.

In Evans' book Partial Differential Equations, 2nd Edition, On page 33, Line 5, Evans wrote that:" Since $V$ is connected and $\overline{V}$ is compact, we can cover $\overline{V}$ by a chain of finitely many ball $\{B_i\}_{i=1}^N,$ each of which has radius $r/2$ and $B_i\cap B_{i-1}\not=\emptyset$ for $i=2,\dots,N.$" My question in this part is that: How to construct such a chain of finitely many balls? This is my first question. For example, suppose that the $\overline{V}$ is as the set below:

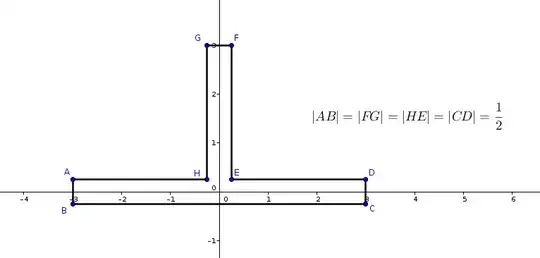
That is to say, $\overline{V}$ is the set bounded by the line segments of $AB, BC, CD, DE, EF, FG, GH$ and $HA.$ And suppose that the radius $r/2$ happens to be $3/2.$ How could I construct a chain of finitely many balls $B_i ~~(i=1,\dots,N)$ of radius $3/2,$ such that $$\overline{V}\subset \cup_{i=1}^N B_i \text{ and } B_i\cap B_{i-1}\not=\emptyset, i=2,\dots,N.$$ I have tried using Heine-Borel Theorem, but is able to find a famyly $\mathcal{F}$ of finitely many balls of radius $3/2$ such that $\mathcal{F}$ covers $\overline{V}.$

Since I have not understand what Evans wrote, I tried to read Gilbarg and Trudinger's book Elliptic Partial Differential Equations of Second Order. On page 16, proof of Theorem 2.5., just below the formula (2.9), they wrote that: "Now let $\Omega'\subset\subset\Omega$ and choose $x_1,x_2\in\overline{\Omega}'$ so that $u(x_1)=\sup_{\Omega'} u, u(x_2)=\inf_{\Omega'} u.$ Let $\Gamma\subset\overline{\Omega'}$ be a closed arc joining $x_1$ and $x_2$ and ... $\Gamma$ can be covered by a finite number $N$ (depending only on $\Omega'$ and $\Omega$) of balls of radius $\mathit{R}.$" As to this part of proof, I have two questions. The first is that: Why $x_1$ and $x_2$ can be joined by an arc $\Gamma?$ Since we know that the connectedness of $\overline{\Omega'}$ does not necessarily imply the pathwise (or arcwise) connectedness of it, I can not find a method to construct such an arc, especially when $x_1 $ or $x_2$ is on $\partial\Omega'.$ My second question is: Why $N$ is not dependent on $x_1, x_2, $ or in another way, on $u?$ Since $x_1, x_2$ have been chosen, then we can construct the arc $\Gamma,$ thus, I think the number $N$ will depend on the coordinates of $x_1, x_2,$ hence on $u.$

Can anyone help me about the above three questions?

Answer 1

Okay, so the first part (the chain of balls) comes from the fact that in a metric space, compactness $\iff$ totally bounded.

The definition of totally bounded, is that $\forall\epsilon\gt 0,\exists x_1,...,x_n: V\subset\cup_{i=1}^n B_\epsilon( x_i)$.

Following directly from this we see that such a chain exists.

To construct one with your example, start at the top, and work your way down in intervals of say $1/2$, taking balls of radius $3/2$, when you get to the bottom, go left taking more balls, then when you get to the end, go all the way right until everything is covered.

Second part:

When we take $\overline{\Omega}'$ this set is compact, which means that a continuous function $u$ must attain it's minimum and maximum on this set, I.e. there are such $x_1,x_2$ that we may construct an arc between.

The reason that the set of finite balls depends on $\Omega', \Omega$ and not $x_1,x_2$ is because the "shape" and "length" of the arc depend on the shape of $\Omega'$, and the shape of $\Omega'$ depends on the shape of "$\Omega$.

Also, the values $x_1,x_2$ are dependant upon $\Omega'$ as well.