14

What is the way to see $S^1\times S^1/(S^1\vee S^1)\simeq S^2$? Even just an intuitive walkthrough. I can't visualize this quotient in my head.

Stefan Hamcke
  • 27,733
Cordelia
  • 143

2 Answers2

19

You can view $S^1\times S^1$ as a torus which can be represented by a rectangle with opposite edges identified with the same orientation (see below).

$\hspace{4.5cm}$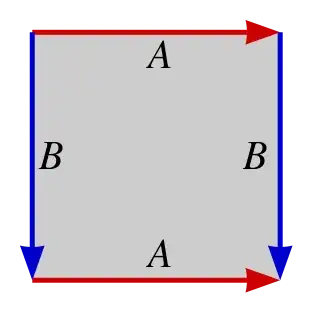enter image description here

Now $S^1\vee S^1$, the wedge sum of two circles, is precisely the boundary of this rectangle (the four corners are identified with a single point which is the point where the two circles are joined). This may be clearer to see on the torus itself (see below).

$\hspace{5.8cm}$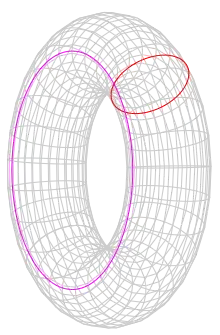enter image description here

So $(S^1\times S^1)/(S^1\vee S^1)$ is the rectangle where we identify the entire boundary with a single point; this is one way to view the two dimensional sphere, as the one-point compactification of $\mathbb{R}^2$.

Michael Albanese
  • 99,526
  • So one copy of $S^1$ (in the wedge sum) is the top and bottom edges of the rectangle, and the other copy of $S^1$ is the left and right edges? – Cordelia May 26 '14 at 05:53
  • That's correct. The images I just included may help to see what's going on. – Michael Albanese May 26 '14 at 05:56
  • Thanks Michael, I understand now. Out of curiosity, I was trying to look at the torus as in your second picture. If we quotient the red circle to a point, it seems like we'd get an earring shaped thing. I couldn't picture a way to then quotient the purple circle to a point, but maybe this is just not the right way to think about it. – Cordelia May 26 '14 at 06:01
  • 1
    @Cordelia You get an earring-shaped thing, and perhaps you should think of collapsing the purple circle as making the "earring hole" smaller and smaller until it's gone. (I think it's better to visualize with the purple circle as the center circle.) –  May 28 '14 at 14:59
  • @MichaelAlbanese: I am curious that can this identification be smooth? – C.F.G Oct 04 '20 at 11:07
  • @C.F.G: What would it mean for the identification to be smooth? You would need a smooth structure on $(S^1\times S^1)/(S^1\vee S^1)$. – Michael Albanese Oct 04 '20 at 20:19
  • @MichaelAlbanese: Isn't the result of above identification a smooth sphere? – C.F.G Oct 04 '20 at 20:23
  • @C.F.G: The sphere certainly has a smooth structure, but I interpreted your question to be regarding the smoothness of the map $(S^1\times S^1)/(S^1\vee S^1) \to S^2$. My point was that it doesn't make sense to talk about a map being smooth or not unless $(S^1\times S^1)/(S^1\vee S^1)$ also has a smooth structure. – Michael Albanese Oct 04 '20 at 20:29
  • @MichaelAlbanese: Of course it should have a smooth structure. Thanks for noticing this. – C.F.G Oct 04 '20 at 20:31
7

Alternatively, one can use the minimal CW complex structure of the sphere to show the following stronger result: $$ (S^n \times S^m) / (S^n \vee S^m) = S^{n+m}. $$

$S^n$ has one $0$-cell and one $n$-cell. $S^m$ has one $0$-cell and one $m$-cell. Hence, the product $S^n \times S^m$ has one cell at each of the dimensions $0$, $n$, $m$, $n + m$.

We can identify $S^n \vee S^m$ with the result of attaching the $n$ and $m$-cells to the $0$-cell. By collapsing $S^n \vee S^m$ to a point, we are left with one $0$-cell and one $(n+m)$-cell. This is $S^{n+m}$.

Ayman Hourieh
  • 39,603