Trigonometric rectangle

Question

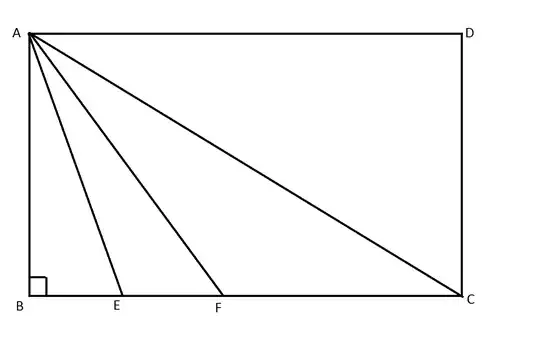
enter image description here

In the rectangle ABCD, $$1. \, BE = EF = FC = AB$$ $$2. \, \angle AEB = \beta , \angle AFB = \alpha , \angle ACB = \theta. $$ Prove that $\alpha + \theta = \beta$.

I have so far obtained that - $$1. \cos\beta = \sin \beta$$ $$2.\cos\alpha = 2\sin\alpha$$ $$3. \cos \theta = 3\sin \theta$$ But I am not able to understand what to do next. Please help.

Your first conclusion -- that $\cos \beta = \sin \beta$ -- appears to be wrong. Can you show us the details? For it to be true, you'd need $BE = AB$, but that's not given. — John Hughes, Jun 05 '14 at 14:13
You are trying to prove $\alpha+\theta=\beta$. But clearly, $\alpha>\beta>\theta$, so how can the statement be true? — David H, Jun 05 '14 at 14:26
@DavidH How did u get that $\alpha> \beta > \theta?$ Kindly please explain — Snehil Sinha, Jun 05 '14 at 14:30
@DavidH yeah I agree with ajotatxe.That was what i had been thinking... — Snehil Sinha, Jun 05 '14 at 14:33
In fact you need to prove that $\arctan 1 = \arctan \dfrac{1}{2}+\arctan \dfrac{1}{3}$. It is nice identity, used by Euler to build series for $\pi$ approximation (see http://mathworld.wolfram.com/EulersMachin-LikeFormula.html). — Oleg567, Jun 05 '14 at 14:33
@ajotatxe Oops, you are right. I had alpha and beta reversed. — David H, Jun 05 '14 at 14:35
See nice visual proof of related problem here: http://math.stackexchange.com/questions/272208/proving-arctan1-arctan2-arctan3-pi/272250#272250 — Oleg567, Jun 05 '14 at 14:36

score 1 · Accepted Answer · answered Jun 05 '14 at 14:23

It is clear that the three angles are acute. Moreover,

$$\tan\beta=2\tan\alpha=3\tan\theta$$

$$\begin{align} \tan(\alpha+\theta)&=\frac{\tan\alpha+\tan\theta}{1-\tan\alpha\tan\theta}\\ &=\frac{\frac56\tan\beta}{1-\frac{\tan^2\beta}6}\\ &=\frac{5\tan\beta}{6-\tan^2\beta} \end{align}$$

So the statement is true only if $6-\tan^2\beta=5$, that is, only if $\tan\beta=1$ or $\beta=45^\circ$.

score 0 · Answer 2 · edited Jun 05 '14 at 14:51

0

You have $\beta= 45degree$ because an isoceles right triangle ABE. then $\tan(\alpha + \theta)$=$(\tan\alpha+\tan\theta)$,$1-\tan\alpha\tan\theta =$(5/6 $\tan\beta$)$1-\tan^2\beta$=$5\tan\beta$ $6-\tan^2\beta$ gives $\tan(\alpha + \theta)=1=\tan\beta$ $\alpha + \theta = \beta$

edited Jun 05 '14 at 14:51

Snehil Sinha

1,179

answered Jun 05 '14 at 14:34

DSinghvi

565

Trigonometric rectangle

2 Answers2