6

Convex hull algorithms are well known. However, in my case, the goal is slightly modified:

Given $N$ points in a plane, construct convex polygon with minimal area so that it contains all points, and there is no point that is closer than given distance $d$ from polygon edges, and number of vertices of such polygon is the same as number of vertices of the convex hull of given points.

In other words, given $N$ sheep:

enter image description here

... find the fence:

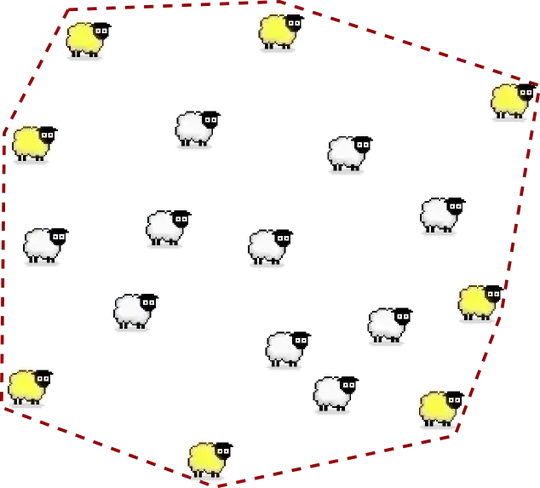
enter image description here

(Sheep can be considered points, but $d$ is still greater than $0$.)

VividD
  • 15,966
  • Interesting problem. Notice that finding the convex hull of disks centered at the sheep is not necessarily optimal. – user7530 Jun 17 '14 at 08:37
  • Probably inflating the convex hull would help? – lisyarus Jun 17 '14 at 08:41
  • @lisyarus Right, that was my first version, in short: find centroid than "inflate" convex hull by moving convex hull edges away from the centroid. However, I was not able to prove that is a correct method. – VividD Jun 17 '14 at 08:45
  • @VividD I didn't mean centroid. You can inflate edges by distance $d$ along their normals. Computing it is some kind of straight skeleton, but it's not obvious for me that the area would be minimal =( – lisyarus Jun 17 '14 at 08:49
  • 2
    Suppose $d=1$. Put four sheep at $(1,0),(-1,0),(0,-0.01)$, and $(0,100)$. Then the inflated convex hull is certainly not optimal $-$ you can do better by truncating the hull at $y=101$ and merging the two lower edges into one. – TonyK Jun 17 '14 at 09:15
  • The following paper describes the convex hull problem where you have discs instead of points, maybe it can be useful to you even if it does not directly solve your problem: RAPPAPORT, David. A convex hull algorithm for discs, and applications. Computational Geometry, 1992, 1.3: 171-187. http://ac.els-cdn.com/092577219290015K/1-s2.0-092577219290015K-main.pdf?_tid=caf266de-075b-11e4-9595-00000aacb35e&acdnat=1404905335_262bfe9a1c5709d46ffe30f517a11bbf – Alessandro Jacopson Jul 09 '14 at 11:59
  • @uvts_cvs, that's great info! – VividD Jul 09 '14 at 19:53

1 Answers1

3

Maybe you can take some ideas from the following paper

RAPPAPORT, David. A convex hull algorithm for discs, and applications. Computational Geometry, 1992, 1.3: 171-187.

where you model each sheep with a circle of radius $d$.

However the paper does not directly solve your problem because the convex hull described in the paper is composed by line segments and arcs of a circle.

Alessandro Jacopson
  • 1,028
  • This is very close to the answer, and there is no better, so I will mark it as an answer. Thanks for great info! – VividD Jul 12 '14 at 18:01