Find normal to ellipse through arbitrary points

Question

I want to find the normal to ellipse through an arbitrary point. There is an array of points located arround a given ellipse (but not on ellipse curve). What I want to find is the normal of each of that point to the ellipse and then find the corresponding point on a given ellipse curve.

The following are given : $P_1, a, b (F_1, F_2)$, ellipse center $C$ is $(0,0)$

What I can generate are the orange lines $ \overline{F_1P_1} $ and $ \overline{F_2P_1}$ Now I can build the bisection line between the orange lines. This should be the normal of a point on an ellipse. ($P_1$ is not on ellipse curve, but I assume that the same assumption is true for an arbitrary point $P_1$ that is located on that normal).

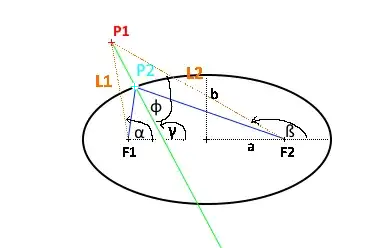
$F_1$ and $F_2$ are found as:

$$e=\sqrt(a^2-b^2)$$ $$F_1=\binom{-e}{0}, F_2 = \binom{+e}{0}$$

$\alpha, \beta, \gamma$ and $\phi$ are calculated as:

$$dx_{1}=P_{1x}-F_{1x}$$ $$dy_{1}=P_{1y}-F_{1y}$$ $$dx_{2}=P_{1x}-F_{2x}$$ $$dy_{2}=P_{1y}-F_{2y}$$ $$l_{1} = \sqrt{(dx_{1}^2+dy_{1}^2)}$$ $$l_{2} = \sqrt{(dx_{2}^2+dy_{2}^2)}$$ $$\alpha = \arccos (dx_{1}/l_{1})$$ $$\beta = \arccos (dx_{2}/l_{2})$$ $$\gamma = {{\alpha + \beta} \over {2}} $$ $$\phi = {{180 - (\alpha \pm \beta)} \over {2}}$$

Now I can generate the normal line. I have to find y-intercept n and slope m. $$f_{n}(x)=m\cdot x+n$$ $$f_{n}(P_{x})=P_{y}$$ $$m=tan(γ)$$ $$n={{f_{n}(x)} - {m\cdot x}}$$

The next step is to find the intersection of this normal with the ellipse. I have no idea how to proceed.

Is the above assumption to find the normal true?

My first idea was to find the intersection point $P_3$ of the normal with the baseline $\overline {F_{1}F_{2}}$ and then generate a point on ellipse like in:

$$x_{n}=C_{x} - P_{3x} + a\cdot \cos t$$ $$y_{n}=C_{y} - P_{3y} + b\cdot \sin t$$

But seems to be wrong. Anyone an idea?

Answer 1

Have you had a look at this https://tcg.mae.cornell.edu/pubs/Pope_FDA_08.pdf It is a collection of various algorithms concerning ellipsoids, distances etc. You may be interested in Section 8 of that book.

Answer 2

I will give an answer to my own question.

The solution was almost right. The question was how to find the intersection points of the normal line with the ellipse. (There can be at most 2 intersection points!)

First we assume that the normal is the bisection line of the two angles. We will calculate y-intercept and slope as described in my initial question.

The solution is to insert line equation into ellipse equation...

$$ {{{x_e}^2} \over {a^2}} + {{{y_e}^2} \over {b^2}} = 1 $$

$$ y_e(x_e) = m \cdot x_e + n $$ ...and then solving monic equation $$ x_e = -\frac{p}{2} \pm \sqrt{\left(\frac{p}{2}\right)^2 - q} $$ First step $$ {{x_e}^2 \over {a^2}} + {{m^2 \cdot {x_e}^2} \over {b^2}} + {{2 \cdot m \cdot n} \over {b^2}} + {{n^2} \over {b^2}} = 1 $$ With $k$ equals to $$ k = \left({1 \over a^2} + {m^2 \over b^2}\right) $$ Results in $$ {x_e}^2 + {{2 \cdot m \cdot n} \over {k \cdot b^2}} \cdot x_e + {{n^2} \over {k \cdot b^2}} - {1 \over k} = 0 $$ Where $p$ and $q$ are... $$ p={{2 \cdot m \cdot n} \over {k \cdot b^2}} $$ $$ q={{n^2} \over {k \cdot b^2}} - {1 \over k} $$