A straight line is drawn through the incentre I of the triangle ABC perpendicular to AI meeting AB, AC in D and E respectively. Prove that BD.CE=ID^2
Asked
Active
Viewed 318 times
1 Answers
4
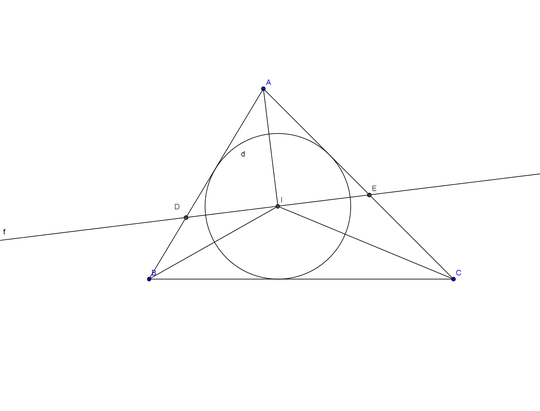 Note $\angle AEI=\angle ADI=90^\circ - \frac{\angle A}{2} = \frac{\angle B}{2}+\frac{\angle C}{2}$.
It follows that $$\angle DIB=\angle ADI-\angle DBI = \frac{\angle C}{2}=\angle ECI.$$
Thus $\triangle DIB$ and $\triangle ECI$ are similar (Having equal angles). The equality follows.
Note $\angle AEI=\angle ADI=90^\circ - \frac{\angle A}{2} = \frac{\angle B}{2}+\frac{\angle C}{2}$.
It follows that $$\angle DIB=\angle ADI-\angle DBI = \frac{\angle C}{2}=\angle ECI.$$
Thus $\triangle DIB$ and $\triangle ECI$ are similar (Having equal angles). The equality follows.
Quang Hoang
- 15,854