5

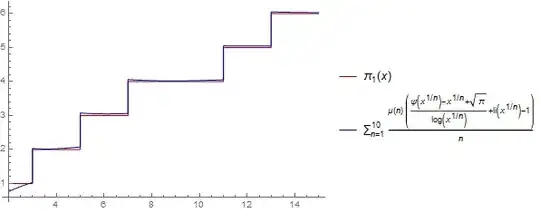
Can $\pi(x)$ be written in terms of $\psi(x)$? I can only seem to approximate it:

$$ \pi(x)\approx\sum_{n=1}^{\infty}\left[\dfrac{\mu(n)}{n}\left(\dfrac{1}{\log(x^{1/n})}\left(\psi(x^{1/n})-x^{1/n}+\sqrt{\pi}\right)+\operatorname{li}(x^{1/n})-1\right)\right] $$

Is there a relationship of equivalence between $\psi(x)$ and $\pi(x)$ (ie, an inversion formula), or can it only approximate it?

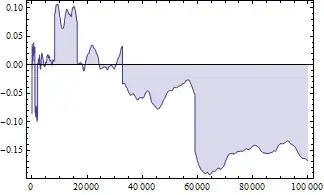
Out of interest I include the difference up to $10^5$ between the RHS and the LHS

enter image description here

and both together for very small $x$

enter image description here

martin
  • 8,998
  • 1
    Well known are the three "explicit formulae" from $(7)$ to $(11);$. The link gives the transformations to go from $;\psi \to \Pi \to \pi;$ i.e. : $$\Pi^(x)=\frac{\psi^(x)}{\log ,x}+\int_2^x\frac{\psi^(t)\ dt}{t,\log^2 t}$$ $$\pi^{}(x)=\sum_{n=1}^{\infty} \frac{\mu(k)}k \Pi^*\left(x^{1/k}\right)$$ After substitution of the first equation (obtained using $(4)$) in the second we get : – Raymond Manzoni Aug 03 '14 at 11:58
  • 1
    \begin{align} \pi^{}(x)&=\sum_{k=1}^{\infty} \frac{\mu(k)}k \left(\int_2^{x^{1/k}}\frac{\psi^(t)\ dt}{t,\log^2 t}+\frac{\psi^*({x^{1/k}})}{\log ,{x^{1/k}}}\right)\ \end{align} You may try some rewriting but the use of $\mathrm{li}$ or $\mathrm{R}$ appeared more fruitful in the past... Hoping this will help anyway, – Raymond Manzoni Aug 03 '14 at 11:59
  • @Raymond Manzoni, thank you! This looks great - thank you for your answer and your link! :) – martin Aug 03 '14 at 14:43
  • 1
    Glad you liked that martin! Fine approximation btw! Cheers, – Raymond Manzoni Aug 03 '14 at 14:52
  • @Raymond Manzoni Thanks! :) – martin Aug 03 '14 at 18:58

1 Answers1

4

There is an easy relation between $\pi(x)$ and $\psi(x)$, namely $$ \pi(x)=\frac{\psi(x)}{\log (x)}+O\left(\frac{x}{\log^2(x)}\right). $$ I am not sure if this is a "better expression". There are very efficient formulas for computing $\pi(x)$, see for example here. There are similarities to your formula in section $4$.

Dietrich Burde
  • 130,978
  • Thanks - this is a bit simpler, but I was wondering whether there is an expression without a $O$ term? NB, I am not really interested in computing $\pi(x)$ from $\psi(x)$, (I believe it is simpler to computer from the $\zeta$ function) I am more interested in the relationship between them. – martin Aug 01 '14 at 07:33
  • Both $\pi(x)$ and $\psi(x)$ can be written in terms of the zeroes of the Riemann Zeta function. Apart from this I don't know how to express one in terms of the other by an exact formula. – Dietrich Burde Aug 01 '14 at 20:44