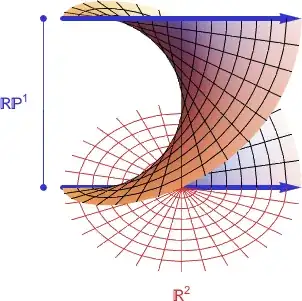
The (real) blow up of $\mathbb{R}^2$ is defined by $\tilde{\mathbb{R}}^2=\{(p,l)\in\mathbb{R}^2\times\mathbb{R}\mathbb{P}^1|p\in l\}$, with the projection $\pi:\tilde{\mathbb{R}}^2\to\mathbb{R}^2$, given by $(p,l)\mapsto p$.
Intuitively speaking, $\tilde{\mathbb{R}}^2$ looks just like the plane, but with many origins, one for every direction.
Question: Is there some familiar 2 dimensional manifold to which $\tilde{\mathbb{R}}^2$ is diffeomorphic?
Answer: Yes! The Moebius band.
Explanation: $\tilde{\mathbb{R}}^2$ can be thought of as the tautological line bundle over $\mathbb{R}\mathbb{P}^1$, whereas the Moebius band is the (only) non-orientable line bundle over $S^1$. Since $\mathbb{R}\mathbb{P}^1$ and $S^1$ are diffeomorphic, so are the blow up of the plane and the Moebius band.
What am I really asking: How would you map the blow up onto the Moebius band? Alternatively, how do you picture these two (different) objects as being the same?
This is an open question, to which there may be many different "correct" answers. I would just like to hear how other people understand this picture.
Bonus question: If you take $S^2$, and blow it up at a point, what do you get? A Klein bottle? A projective plane? Something else? $S^2$ is the one point compactification of $\mathbb{R}^2$, so the blow up should be some one point compactification of the Moebius band. What is it? And again, how would you picture that?