for $x\in (0,\infty)$ show $f(x)=x^4$ is convex. I know it is convex since $f''(x)>0$ . How can we show by using definition? do we have to use Let L be linear space. $t\in[0,1],y\in L,f(xt+y(1-t))=(xt)^4+4(xt)^3((1-t)y)^1+6(xt)^2((1-t)y)^2+4(xt)(((1-t)y)^3+((1-t)y)^4$
edit: $(xt)^4+4(xt)^3((1-t)y)^1+6(xt)^2((1-t)y)^2+4(xt)(((1-t)y)^3+((1-t)y)^4\le tf(x)+4tf(x)+10tf(x)(1-t)f(y)+(1-t)f(y)$
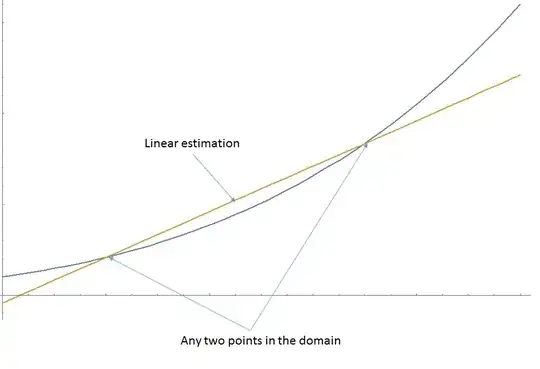 Now all you have to check is that for any ${x_{\rm{i}}} > 0
% MathType!MTEF!2!1!+-
% feaagKart1ev2aaatCvAUfKttLearuqr1ngBPrgarmqr1ngBPrgitL
% xBI9gBamXvP5wqSXMqHnxAJn0BKvguHDwzZbqegm0B1jxALjhiov2D
% aeHbuLwBLnhiov2DGi1BTfMBaebbfv3ySLgzGueE0jxyaibaieYlf9
% irVeeu0dXdh9vqqj-hEeeu0xXdbba9frFj0-OqFfea0dXdd9vqaq-J
% frVkFHe9pgea0dXdar-Jb9hs0dXdbPYxe9vr0-vr0-vqpWqaaeaabi
% GaciaacaqabeaadaabauaaaOqaaiabdIha4naaBaaaleaacqqGPbqA
% aeqaaOGaeyOpa4JaeGimaadaaa!43FD!
$ and ${x_{\rm{f}}} > {x_{\rm{i}}}
% MathType!MTEF!2!1!+-
% feaagKart1ev2aaatCvAUfKttLearuqr1ngBPrgarmqr1ngBPrgitL
% xBI9gBamXvP5wqSXMqHnxAJn0BKvguHDwzZbqegm0B1jxALjhiov2D
% aeHbuLwBLnhiov2DGi1BTfMBaebbfv3ySLgzGueE0jxyaibaieYlf9
% irVeeu0dXdh9vqqj-hEeeu0xXdbba9frFj0-OqFfea0dXdd9vqaq-J
% frVkFHe9pgea0dXdar-Jb9hs0dXdbPYxe9vr0-vr0-vqpWqaaeaabi
% GaciaacaqabeaadaabauaaaOqaaiabdIha4naaBaaaleaacqqGMbGz
% aeqaaOGaeyOpa4JaemiEaG3aaSbaaSqaaiabbMgaPbqabaaaaa!4607!
$ and $\xi = (1 - t){x_{\rm{i}}} + t{x_{\rm{f}}}
% MathType!MTEF!2!1!+-
% feaagKart1ev2aaatCvAUfKttLearuqr1ngBPrgarmqr1ngBPrgitL
% xBI9gBamXvP5wqSXMqHnxAJn0BKvguHDwzZbqegm0B1jxALjhiov2D
% aeHbuLwBLnhiov2DGi1BTfMBaebbfv3ySLgzGueE0jxyaibaieYlf9
% irVeeu0dXdh9vqqj-hEeeu0xXdbba9frFj0-OqFfea0dXdd9vqaq-J
% frVkFHe9pgea0dXdar-Jb9hs0dXdbPYxe9vr0-vr0-vqpWqaaeaabi
% GaciaacaqabeaadaabauaaaOqaaiabe67a4jabg2da9iabcIcaOiab
% igdaXiabgkHiTiabdsha0jabcMcaPiabdIha4naaBaaaleaacqqGPb
% qAaeqaaOGaey4kaSIaemiDaqNaemiEaG3aaSbaaSqaaiabbAgaMbqa
% baaaaa!4F1B!
$ (such that $0 < t < 1
% MathType!MTEF!2!1!+-
% feaagKart1ev2aaatCvAUfKttLearuqr1ngBPrgarmqr1ngBPrgitL
% xBI9gBamXvP5wqSXMqHnxAJn0BKvguHDwzZbqegm0B1jxALjhiov2D
% aeHbuLwBLnhiov2DGi1BTfMBaebbfv3ySLgzGueE0jxyaibaieYlf9
% irVeeu0dXdh9vqqj-hEeeu0xXdbba9frFj0-OqFfea0dXdd9vqaq-J
% frVkFHe9pgea0dXdar-Jb9hs0dXdbPYxe9vr0-vr0-vqpWqaaeaabi
% GaciaacaqabeaadaabauaaaOqaaiabicdaWiabgYda8iabdsha0jab
% gYda8iabigdaXaaa!4456!
$), $$f({x_{\rm{i}}}) + \frac{{f({x_{\rm{f}}}) - f({x_{\rm{i}}})}}{{{x_{\rm{f}}} - {x_{\rm{i}}}}}(\xi - {x_{\rm{i}}}) > f(\xi )
% MathType!MTEF!2!1!+-
% feaagKart1ev2aaatCvAUfKttLearuqr1ngBPrgarmqr1ngBPrgitL
% xBI9gBamXvP5wqSXMqHnxAJn0BKvguHDwzZbqegm0B1jxALjhiov2D
% aeHbuLwBLnhiov2DGi1BTfMBaebbfv3ySLgzGueE0jxyaibaieYlf9
% irVeeu0dXdh9vqqj-hEeeu0xXdbba9frFj0-OqFfea0dXdd9vqaq-J
% frVkFHe9pgea0dXdar-Jb9hs0dXdbPYxe9vr0-vr0-vqpWqaaeaabi
% GaciaacaqabeaadaabauaaaOqaaiabdAgaMjabcIcaOiabdIha4naa
% BaaaleaacqqGPbqAaeqaaOGaeiykaKIaey4kaSYaaSaaaeaacqWGMb
% GzcqGGOaakcqWG4baEdaWgaaWcbaGaeeOzaygabeaakiabcMcaPiab
% gkHiTiabdAgaMjabcIcaOiabdIha4naaBaaaleaacqqGPbqAaeqaaO
% GaeiykaKcabaGaemiEaG3aaSbaaSqaaiabbAgaMbqabaGccqGHsisl
% cqWG4baEdaWgaaWcbaGaeeyAaKgabeaaaaGccqGGOaakcqaH+oaEcq
% GHsislcqWG4baEdaWgaaWcbaGaeeyAaKgabeaakiabcMcaPiabg6da
% +iabdAgaMjabcIcaOiabe67a4jabcMcaPaaa!6738!
$$. Replacing the function that you have asked yields proving that $${x_{\rm{f}}}^4 - ((1 - t){x_{\rm{i}}}^4 + t{x_{\rm{f}}}^4) + t({x_{\rm{f}}}^4 - {x_{\rm{i}}}^4) > 0
% MathType!MTEF!2!1!+-
% feaagKart1ev2aaatCvAUfKttLearuqr1ngBPrgarmqr1ngBPrgitL
% xBI9gBamXvP5wqSXMqHnxAJn0BKvguHDwzZbqegm0B1jxALjhiov2D
% aeHbuLwBLnhiov2DGi1BTfMBaebbfv3ySLgzGueE0jxyaibaieYlf9
% irVeeu0dXdh9vqqj-hEeeu0xXdbba9frFj0-OqFfea0dXdd9vqaq-J
% frVkFHe9pgea0dXdar-Jb9hs0dXdbPYxe9vr0-vr0-vqpWqaaeaabi
% GaciaacaqabeaadaabauaaaOqaaiabdIha4naaBaaaleaacqqGMbGz
% aeqaaOWaaWbaaSqabeaacqaI0aanaaGccqGHsislcqGGOaakcqGGOa
% akcqaIXaqmcqGHsislcqWG0baDcqGGPaqkcqWG4baEdaWgaaWcbaGa
% eeyAaKgabeaakmaaCaaaleqabaGaeGinaqdaaOGaey4kaSIaemiDaq
% NaemiEaG3aaSbaaSqaaiabbAgaMbqabaGcdaahaaWcbeqaaiabisda
% 0aaakiabcMcaPiabgUcaRiabdsha0jabcIcaOiabdIha4naaBaaale
% aacqqGMbGzaeqaaOWaaWbaaSqabeaacqaI0aanaaGccqGHsislcqWG
% 4baEdaWgaaWcbaGaeeyAaKgabeaakmaaCaaaleqabaGaeGinaqdaaO
% GaeiykaKIaeyOpa4JaeGimaadaaa!64D0!
$$. Note that the above inequality is trivially true when the domain is restricted to the positive real line, so the function is convex indeed.
Now all you have to check is that for any ${x_{\rm{i}}} > 0
% MathType!MTEF!2!1!+-
% feaagKart1ev2aaatCvAUfKttLearuqr1ngBPrgarmqr1ngBPrgitL
% xBI9gBamXvP5wqSXMqHnxAJn0BKvguHDwzZbqegm0B1jxALjhiov2D
% aeHbuLwBLnhiov2DGi1BTfMBaebbfv3ySLgzGueE0jxyaibaieYlf9
% irVeeu0dXdh9vqqj-hEeeu0xXdbba9frFj0-OqFfea0dXdd9vqaq-J
% frVkFHe9pgea0dXdar-Jb9hs0dXdbPYxe9vr0-vr0-vqpWqaaeaabi
% GaciaacaqabeaadaabauaaaOqaaiabdIha4naaBaaaleaacqqGPbqA
% aeqaaOGaeyOpa4JaeGimaadaaa!43FD!
$ and ${x_{\rm{f}}} > {x_{\rm{i}}}
% MathType!MTEF!2!1!+-
% feaagKart1ev2aaatCvAUfKttLearuqr1ngBPrgarmqr1ngBPrgitL
% xBI9gBamXvP5wqSXMqHnxAJn0BKvguHDwzZbqegm0B1jxALjhiov2D
% aeHbuLwBLnhiov2DGi1BTfMBaebbfv3ySLgzGueE0jxyaibaieYlf9
% irVeeu0dXdh9vqqj-hEeeu0xXdbba9frFj0-OqFfea0dXdd9vqaq-J
% frVkFHe9pgea0dXdar-Jb9hs0dXdbPYxe9vr0-vr0-vqpWqaaeaabi
% GaciaacaqabeaadaabauaaaOqaaiabdIha4naaBaaaleaacqqGMbGz
% aeqaaOGaeyOpa4JaemiEaG3aaSbaaSqaaiabbMgaPbqabaaaaa!4607!
$ and $\xi = (1 - t){x_{\rm{i}}} + t{x_{\rm{f}}}
% MathType!MTEF!2!1!+-
% feaagKart1ev2aaatCvAUfKttLearuqr1ngBPrgarmqr1ngBPrgitL
% xBI9gBamXvP5wqSXMqHnxAJn0BKvguHDwzZbqegm0B1jxALjhiov2D
% aeHbuLwBLnhiov2DGi1BTfMBaebbfv3ySLgzGueE0jxyaibaieYlf9
% irVeeu0dXdh9vqqj-hEeeu0xXdbba9frFj0-OqFfea0dXdd9vqaq-J
% frVkFHe9pgea0dXdar-Jb9hs0dXdbPYxe9vr0-vr0-vqpWqaaeaabi
% GaciaacaqabeaadaabauaaaOqaaiabe67a4jabg2da9iabcIcaOiab
% igdaXiabgkHiTiabdsha0jabcMcaPiabdIha4naaBaaaleaacqqGPb
% qAaeqaaOGaey4kaSIaemiDaqNaemiEaG3aaSbaaSqaaiabbAgaMbqa
% baaaaa!4F1B!
$ (such that $0 < t < 1
% MathType!MTEF!2!1!+-
% feaagKart1ev2aaatCvAUfKttLearuqr1ngBPrgarmqr1ngBPrgitL
% xBI9gBamXvP5wqSXMqHnxAJn0BKvguHDwzZbqegm0B1jxALjhiov2D
% aeHbuLwBLnhiov2DGi1BTfMBaebbfv3ySLgzGueE0jxyaibaieYlf9
% irVeeu0dXdh9vqqj-hEeeu0xXdbba9frFj0-OqFfea0dXdd9vqaq-J
% frVkFHe9pgea0dXdar-Jb9hs0dXdbPYxe9vr0-vr0-vqpWqaaeaabi
% GaciaacaqabeaadaabauaaaOqaaiabicdaWiabgYda8iabdsha0jab
% gYda8iabigdaXaaa!4456!
$), $$f({x_{\rm{i}}}) + \frac{{f({x_{\rm{f}}}) - f({x_{\rm{i}}})}}{{{x_{\rm{f}}} - {x_{\rm{i}}}}}(\xi - {x_{\rm{i}}}) > f(\xi )
% MathType!MTEF!2!1!+-
% feaagKart1ev2aaatCvAUfKttLearuqr1ngBPrgarmqr1ngBPrgitL
% xBI9gBamXvP5wqSXMqHnxAJn0BKvguHDwzZbqegm0B1jxALjhiov2D
% aeHbuLwBLnhiov2DGi1BTfMBaebbfv3ySLgzGueE0jxyaibaieYlf9
% irVeeu0dXdh9vqqj-hEeeu0xXdbba9frFj0-OqFfea0dXdd9vqaq-J
% frVkFHe9pgea0dXdar-Jb9hs0dXdbPYxe9vr0-vr0-vqpWqaaeaabi
% GaciaacaqabeaadaabauaaaOqaaiabdAgaMjabcIcaOiabdIha4naa
% BaaaleaacqqGPbqAaeqaaOGaeiykaKIaey4kaSYaaSaaaeaacqWGMb
% GzcqGGOaakcqWG4baEdaWgaaWcbaGaeeOzaygabeaakiabcMcaPiab
% gkHiTiabdAgaMjabcIcaOiabdIha4naaBaaaleaacqqGPbqAaeqaaO
% GaeiykaKcabaGaemiEaG3aaSbaaSqaaiabbAgaMbqabaGccqGHsisl
% cqWG4baEdaWgaaWcbaGaeeyAaKgabeaaaaGccqGGOaakcqaH+oaEcq
% GHsislcqWG4baEdaWgaaWcbaGaeeyAaKgabeaakiabcMcaPiabg6da
% +iabdAgaMjabcIcaOiabe67a4jabcMcaPaaa!6738!
$$. Replacing the function that you have asked yields proving that $${x_{\rm{f}}}^4 - ((1 - t){x_{\rm{i}}}^4 + t{x_{\rm{f}}}^4) + t({x_{\rm{f}}}^4 - {x_{\rm{i}}}^4) > 0
% MathType!MTEF!2!1!+-
% feaagKart1ev2aaatCvAUfKttLearuqr1ngBPrgarmqr1ngBPrgitL
% xBI9gBamXvP5wqSXMqHnxAJn0BKvguHDwzZbqegm0B1jxALjhiov2D
% aeHbuLwBLnhiov2DGi1BTfMBaebbfv3ySLgzGueE0jxyaibaieYlf9
% irVeeu0dXdh9vqqj-hEeeu0xXdbba9frFj0-OqFfea0dXdd9vqaq-J
% frVkFHe9pgea0dXdar-Jb9hs0dXdbPYxe9vr0-vr0-vqpWqaaeaabi
% GaciaacaqabeaadaabauaaaOqaaiabdIha4naaBaaaleaacqqGMbGz
% aeqaaOWaaWbaaSqabeaacqaI0aanaaGccqGHsislcqGGOaakcqGGOa
% akcqaIXaqmcqGHsislcqWG0baDcqGGPaqkcqWG4baEdaWgaaWcbaGa
% eeyAaKgabeaakmaaCaaaleqabaGaeGinaqdaaOGaey4kaSIaemiDaq
% NaemiEaG3aaSbaaSqaaiabbAgaMbqabaGcdaahaaWcbeqaaiabisda
% 0aaakiabcMcaPiabgUcaRiabdsha0jabcIcaOiabdIha4naaBaaale
% aacqqGMbGzaeqaaOWaaWbaaSqabeaacqaI0aanaaGccqGHsislcqWG
% 4baEdaWgaaWcbaGaeeyAaKgabeaakmaaCaaaleqabaGaeGinaqdaaO
% GaeiykaKIaeyOpa4JaeGimaadaaa!64D0!
$$. Note that the above inequality is trivially true when the domain is restricted to the positive real line, so the function is convex indeed.