Solve the "two trains and a fly" problem the hard way

Question

Few days ago, I was asked the following question:

There are $2$ cities. city $A$ and city $B$ with distance $d$=600km
There are $2$ trains with speed of $vt$ = 100km/h.
There is $1$ fly with speed of $vf$ = 300km/h.

The question:
Train 1 goes from city A to city B , while Train 2 goes in the opposite direction.(both start at the same time). the fly starts from train 1 and go to train 2 , than back to train 1 , than back to train 2...etc...

What is the distance that the fly passes till the trains cross each other ?

The answer is simple - it takes 3 hours for the train to cross -> fly was running 900km($300 \times 3$).

I was wondering on the "hard" way of solving this problem by actually calculating the distance the fly pass on each stage. It appears to be the sum of a (finite?) series of the distances.

Could you help me solve this problem the "hard way" ?

Answer 1

If the trains are distance $d$ apart and the fly starts on one train then it takes $d/(vt+vf)=d/400$ hours for the fly to reach the other train, and at that time the trains are $(2 vt) d/400 = d/2$ km apart, the fly having flown $(3 d/4)$ km. So after each trip from train to train the trains close by half the distance, so the fly travels $3 d/4+3d/8+3d/16+\cdots$, or $3d/4 \sum_{n=0}^\infty 1/2^n$. Now, the series $\sum_{n=0}^\infty 1/2^n$ is a geometric series of the form $\sum_{n=0}^\infty \alpha^n$ which if $|\alpha|<1$ equals $1/(1-\alpha)$, or in our case 2. So in our case, as $d=600$ the fly travels $2 * 3 * 600 / 4 = 900$km.

The story of von Neumann saying that he summed the series, always struck me as a completely reasonable approach. If you stare at geometric series all day, it is easy to recognize this problem as a series problem, and it is not much more difficult than using the "trick". In a certain sense, the "trick" is implicit in the formula.

Answer 2

For the $n^\text{th}$ leg of the journey of the fly:

• let $t_n$ be the time taken

• at the start of this leg:

  • the total distance already travelled by both trains is $\quad 2v_t\sum_{i=1}^{n-1}t_i$
  • the distance between the fly and the opposite train is $\quad d-2v_t\sum_{i=1}^{n-1}t_i$

Using Speed $\times$ Time = Distance, we have

$$\begin{align} (v_t+v_f)t_n&=d-2v_t\sum_{i=1}^{n-1}t_i\\ 400t_n&=600-200\sum_{i=1}^{n-1}t_i\\ 2t_n&=3-\sum_{i=1}^{n-1}t_i\\ \end{align}$$

Subtracting consecutive terms gives $$\begin{align}2(t_n-t_{n-1})&=-t_{n-1}\\ t_n&=\frac 12 t_{n-1}\end{align} $$ which is a geometric series.

Hence $$t_n=\left(\frac 1{2^{n-1}} \right)t_1=\frac 32 \left(\frac 1{2^{n-1}} \right)=\frac 3{2^n}$$ and distance covered by the fly on the $n^{\text{th}}$ leg is $$s_n=300t_n=\frac {900}{2^n}$$

Total distance travelled by fly, $$\begin{align}S&=s_1+s_2+...+s_n+...\\ &=450+225+...+\frac {900}{2^n}+...\\ &=900\sum_{i=1}^{n}\frac 1{2^i} \\ &=900\end{align}$$

Answer 3

This is an old post. So, I hope it is not too late to answer. I have come up with a solution for the fly & trains problem that allows for the trains to travel at different speeds and for the fly to travel at different speeds depending on its direction, and which leads to the "short cut" solution in the simplest cases. This solution is also computationally simple.

Assume that the trains start a distance d apart, that the train the fly is on initially (the "s-train") travels at speed s, while the other train (the "r-train") travels at speed r. Furthermore assume that when the fly flies from the s-train to the r-train it does so at speed f, and when it flies from the r-train to the s-train it does so at speed e. For reasonableness we must also assume that f>s and e>r.

I will refer to each flight of the fly from one train to another as a "leg" of its journey. By an "sr-leg" I mean one in which the fly goes from the s-train to the r-train, and by an "rs-leg" I mean one in which the fly goes from the r-train to the s-train. 

For an sr-leg with initial inter-train distance D, the duration of that leg will be D/(f+r), the length of the leg (distance the fly travels) will be fD/(f+r), during which the s-train will have advanced sD/(f+r), and thus the inter-train distance of the next leg will be (f-s)D/(f+r).

Similarly, for an rs-leg with initial inter-train distance D, the duration of that leg will be D/(e+s), the length of that leg will be eD/(e+s), during which the r-train will have advanced rD/(e+s), and thus the inter-train distance of the next leg will be (e-r)D/(e+s).

Define the ratios of the lengths of successive legs, 

a = (f-s)/(f+r),

b = (e-r)/(e+s),

and the ratios of the fly's (ground)speed to the relative speed of the fly and the train it is flying to,

g = f/(f+r),

h = e/(e+s).

Then it can be seen that the inter-train distances of successive legs is

 d, da,  dab,  da^2b,  da^2b^2,  da^3b^2,  da^3b^3,  ...

and thus that the lengths of successive legs is 

gd,  hda,  gdab,  hda^2b,  gda^2b^2, hda^3b^2,  gda^3b^3, ...

So that  the total distance the fly travels is

 gd[1 + (ab) + (ab)^2 + (ab)^3 ...] + hda[1 + (ab) + (ab)^2 + (ab)^3 ...] 

and since a<1 and b<1, and thus ab<1, the above equals

= d(g+ha)/(1-ab).

This is the general solution to the problem. 

If we assume, per the original problem, that both trains travel at the same speed s, and that the fly always travels at speed f, the above expression reduces to fd/2s. 

If we assume that the trains travel at different speeds s and r, but the fly always travels as speed f, the above expression reduces to fd/(r+s).

If we assume there is wind with speed w parallel to the track in the direction from the s-train to the r-train, so that the fly's groundspeed is f+w on the sr-legs and f-w on the rs-legs, and also assume that r=s, then the above expression reduces to (d/2s)(f + (s-w)(w/f)), which reduces to the solution of the original problem fd/2s when w=0, but also, interestingly, when w=s.

The general solution can be written as

d(2ef - es + fs) / ((e+f)(r+s)) 

or more symmetrically as

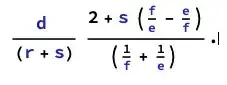
The term on the left d/(r+s) is the total time the fly travels (before the trains crash), while the term on the right is apparently the time-averaged speed of the fly.