Limit of a Riemann Sum and Integral

Question

I've been trying to solve this problem, but I haven't been able to calculate the exact limit, I've just been able to find some boundaries. I hope you guys can help me with it.

Let $f:[0,1] \to \mathbb{R}$ a differentiable function with a continuous derivative, calculate: $$\lim_{n\to \infty}\left(\sum_{k=1}^nf\left(\frac{k}{n}\right)-n\int_0^1f(x)dx\right) $$ I tried using Mean Value Theorem for derivatives and integrals and I got that $$\lim_{n\to \infty}\left(\sum_{k=1}^nf\left(\frac{k}{n}\right)-n\int_0^1f(x)dx\right)=\lim_{n\to \infty}\left(\sum_{k=1}^nf'\left(x_k**\right)(\frac{k}{n}-x_k*)\right) $$ Where $x_k*\in [\frac{k-1}{n},\frac{k}{n}]$ and $x_k**\in [x_k*,\frac{k}{n}]$, which looks like a Riemann Sum but I'm not sure if it's a Riemann Sum of $f'$ from $0$ to $1$, if this was true I believe the limit is $f(1)-f(0)$ but I'm not really sure about this.

Edit: fixed some typos with the $\frac{k}{n}$.

Edit 2: $k$ starts from $1$ not $0$.

Answer 1

Let $$ x_n=\sum_{k=0}^nf\left(\frac{k}{n}\right)-n\int_0^1f(x)dx $$

We will use the following result:

Lemma If $g:[0,1]\to\mathbb{R}$ is a continuously differentiable function. Then $$ \frac{g(0)+g(1)}{2}-\int_0^1g(x)dx= \int_{0}^1\left(x-\frac{1}{2}\right)g'(x)dx. $$ Indeed, this is just integration by parts: $$\eqalign{ \int_{0}^1\left(x-\frac{1}{2}\right)g'(x)dx &=\left.\left(x-\frac{1}{2}\right)g(x)\right]_{x=0}^{x=1} -\int_0^1g(x)dx\cr &=\frac{g(1)+g(0)}{2}-\int_0^1g(x)dx }$$

Now applying this to the functions $x\mapsto f\left(\frac{k+x}{n}\right)$ for $k=0,1,\ldots,n-1$ and adding the resulting inequalities we obtain $$ x_n-\frac{f(0) +f(1)}{2} = \int_0^1\left(x-\frac{1}{2}\right)H_n(x)dx\tag{1} $$ where, $$ H_n(x)=\frac{1}{n}\sum_{k=0}^{n-1}f'\left(\frac{k+x}{n}\right) $$ Clearly for every $x$, $H_n(x)$ is a Riemann sum of the function continuous $f'$, hence $$ \forall\,x\in[0,1],\quad\lim_{n\to\infty}H_n(x)=\int_0^1f'(t)dt $$ Moreover, $| H_n(x)|\leq\sup_{[0,1]}|f'|$. So, taking the limit in $(1)$ and applying the Dominated Convergence Theorem, we obtain $$ \lim_{n\to\infty}\left(x_n-\frac{f(0) +f(1)}{2}\right)= \left(\int_0^1f'(t)dt\right)\int_0^1\left(x-\frac{1}{2}\right)dx=0. $$ This proves that $$ \lim_{n\to\infty}x_n=\frac{f(0) +f(1)}{2} $$

And consequently $$ \lim_{n\to\infty}\left(\sum_{k=\color{red}{1}}^nf\left(\frac{k}{n}\right)-n\int_0^1f(x)dx\right)=\frac{f(1)-f(0)}{2} $$

Answer 2

$\newcommand{\angles}[1]{\left\langle\, #1 \,\right\rangle} \newcommand{\braces}[1]{\left\lbrace\, #1 \,\right\rbrace} \newcommand{\bracks}[1]{\left\lbrack\, #1 \,\right\rbrack} \newcommand{\ceil}[1]{\,\left\lceil\, #1 \,\right\rceil\,} \newcommand{\dd}{{\rm d}} \newcommand{\ds}[1]{\displaystyle{#1}} \newcommand{\expo}[1]{\,{\rm e}^{#1}\,} \newcommand{\fermi}{\,{\rm f}} \newcommand{\floor}[1]{\,\left\lfloor #1 \right\rfloor\,} \newcommand{\half}{{1 \over 2}} \newcommand{\ic}{{\rm i}} \newcommand{\iff}{\Longleftrightarrow} \newcommand{\imp}{\Longrightarrow} \newcommand{\pars}[1]{\left(\, #1 \,\right)} \newcommand{\partiald}[3][]{\frac{\partial^{#1} #2}{\partial #3^{#1}}} \newcommand{\pp}{{\cal P}} \newcommand{\root}[2][]{\,\sqrt[#1]{\vphantom{\large A}\,#2\,}\,} \newcommand{\sech}{\,{\rm sech}} \newcommand{\sgn}{\,{\rm sgn}} \newcommand{\totald}[3][]{\frac{{\rm d}^{#1} #2}{{\rm d} #3^{#1}}} \newcommand{\verts}[1]{\left\vert\, #1 \,\right\vert}$ $\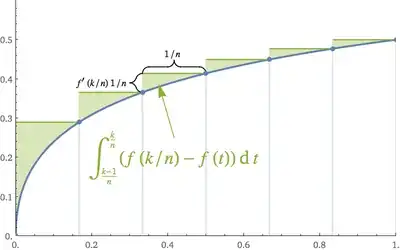ds{\lim_{n\ \to\ \infty}\bracks{\sum_{k = 1}^{n}\fermi\pars{k \over n} -n\int_{0}^{1}\fermi\pars{x}\,\dd x}:\ {\large ?}}$.

$\ds{\tt\mbox{This is an application of}}$ Abel-Plana formula:

\begin{align}&\color{#c00000}{\sum_{k = 1}^{n}\fermi\pars{k \over n}} =\sum_{k = 0}^{n - 1}\fermi\pars{k + 1 \over n} =\sum_{k = 0}^{\infty}\bracks{\fermi\pars{k + 1 \over n} -\fermi\pars{k + n + 1 \over n}} \\[5mm]&=\int_{0}^{\infty} \bracks{\fermi\pars{x + 1 \over n} - \fermi\pars{x + n + 1 \over n}}\,\dd x +\half\bracks{\fermi\pars{1 \over n} - \fermi\pars{n + 1 \over n}} \\[3mm]&+\color{#00f}{\ic\int_{0}^{\infty} \bracks{\fermi\pars{\ic x + 1 \over n} - \fermi\pars{\ic x + n + 1 \over n} -\fermi\pars{-\ic x + 1 \over n} + \fermi\pars{-\ic x + n + 1 \over n}}\times} \\[3mm]&\color{#00f}{\dd x \over \expo{2\pi x} - 1} \\[5mm]&=n\int_{1/n}^{\infty}\fermi\pars{x}\,\dd x -\int_{1 + 1/n}^{\infty}\fermi\pars{x}\,\dd x +\half\bracks{\fermi\pars{1 \over n} - \fermi\pars{n + 1 \over n}} + \color{#00f}{"\mbox{the blue term}"} \\[3mm]&=n\int_{1/n}^{1 + 1/n}\fermi\pars{x}\,\dd x +\half\bracks{\fermi\pars{1 \over n} - \fermi\pars{n + 1 \over n}} + \color{#00f}{"\mbox{the blue term}"} \\[3mm]&=n\int_{0}^{1}\fermi\pars{x}\,\dd x -n\int_{0}^{1/n}\fermi\pars{x}\,\dd x + n\int_{1}^{1 + 1/n}\fermi\pars{x}\,\dd x +\half\bracks{\fermi\pars{1 \over n} - \fermi\pars{n + 1 \over n}} \\[3mm]&\mbox{}+ \color{#00f}{"\mbox{the blue term}"} \end{align}

Since $\ds{\lim_{n\ \to\ \infty}\color{#00f}{\pars{"\mbox{the blue term}"}} = 0}$ and $\ds{\lim_{n\ \to\ \infty}n\int_{0}^{1/n}\fermi\pars{x}\,\dd x = \fermi\pars{0}}$ and $\ds{\lim_{n\ \to\ \infty}n\int_{1}^{1 + 1/n}\fermi\pars{x}\,\dd x = \fermi\pars{1}}$:

\begin{align} &\color{#66f}{\large\lim_{n\ \to\ \infty}\bracks{% \sum_{k = 1}^{n}\fermi\pars{k \over n} - n\int_{0}^{1}\fermi\pars{x}\,\dd x}} \\[3mm]&=-\fermi\pars{0} + \fermi\pars{1} +\half\bracks{\fermi\pars{0} - \fermi\pars{1}} =\color{#66f}{\large{\fermi\pars{1} - \fermi\pars{0} \over 2}} \end{align}

Answer 3

This was brought up recently in chat and I wrote this up. This question seemed like a good home.

---

As hinted in the following diagram

$$ \int_{\frac{k-1}n}^{\frac{k}n}(f(k/n)-f(t))\,\mathrm{d}t\sim\frac{f'(k/n)}{2n^2}\tag1 $$ In fact, integration by parts and the mean value theorem yield for some $\xi\in\left(\frac{k-1}n,\frac{k}n\right)$: $$ \begin{align} \int_{\frac{k-1}n}^{\frac{k}n}(f(k/n)-f(t))\,\mathrm{d}t &=\int_{\frac{k-1}n}^{\frac{k}n}\left(t-\frac{k-1}n\right)f'(t)\,\mathrm{d}t\tag{2a}\\ &=\frac{f'(k/n)}{2n^2}-\int_{\frac{k-1}n}^{\frac{k}n}\frac12\left(t-\frac{k-1}n\right)^2f''(t)\,\mathrm{d}t\tag{2b}\\ &=\frac{f'(k/n)}{2n^2}-\frac1{6n^3}f''(\xi)\tag{2c} \end{align} $$ Explanation:
$\text{(2a)}$: Integration by Parts
$\text{(2b)}$: Integration by Parts
$\text{(2c)}$: Mean Value Theorem

Therefore, $$ \begin{align} \lim_{n\to\infty}\left(\sum_{k=1}^nf(k/n)-n\int_0^1f(t)\,\mathrm{d}t\right) &=\lim_{n\to\infty}\left(n\sum_{k=1}^n\int_{\frac{k-1}n}^{\frac{k}n}(f(k/n)-f(t))\,\mathrm{d}t\right)\tag{3a}\\ &=\lim_{n\to\infty}\sum_{k=1}^n\frac12f'(k/n)\,\frac1n\tag{3b}\\ &=\frac12(f(1)-f(0))\tag{3c} \end{align} $$ Explanation:
$\text{(3a)}$: break up the integral and move the sum inside the integral
$\text{(3b)}$: apply $(2)$
$\text{(3c)}$: apply Riemann Summation

Answer 4

From the error analysis paragraph in the Wikipedia page for the Trapezoidal rule we have that the limit is: $$\frac{f(0)+f(1)}{2}.$$