22

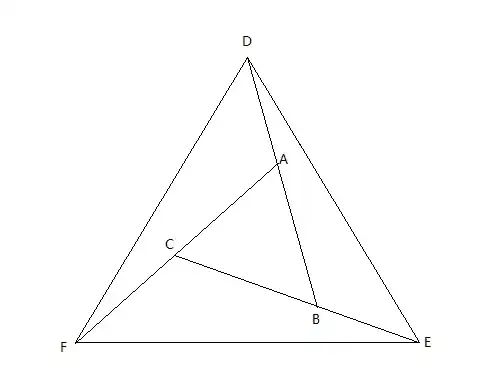
enter image description here

In the figure, AD=BE=CF. Moreover, DEF is an equilateral triangle. Must ABC be equilateral?

Steven
  • 221
  • 6
    Is it also given that $B, A, D$ are collinear, $A, C, F$ are collinear, and $C, B, E$ are collinear? – David K Sep 07 '14 at 15:54
  • Use the following BD = AB + BD ; BE ; $\angle DBE = 120^\circ$ and try using SAS congruency. – Soham Sep 07 '14 at 17:27

2 Answers2

17

Yes, suppose that $\angle A$ is the largest angle of $\triangle ABC$, then $BC$ is the max side. Thus $$CE=\max(CE,FA,BD).$$ That is $$\angle CFE=\max(\angle ADF,\angle CFE,\angle BED).$$ or $$\angle CFD=\min(\angle CFD,\angle BDE,\angle CEF).$$

It follows that in $\triangle ABC$, $$\angle A=\angle ADF+\angle CFD\leq \angle CFE+\angle CEF=\angle C,$$ or $\angle A=\angle C$.

Quang Hoang
  • 15,854
  • 1
    I was trying to state the same by using the cosine theorem, but this approach is much more efficient. Nice. (+1) – Jack D'Aurizio Sep 07 '14 at 16:00
  • Could you just expand the last step (angle A $\le$ angle C)? – almagest Sep 07 '14 at 16:05
  • 1
    This is just an insanely good answer +1 – Asimov Sep 07 '14 at 16:07
  • Jack: I actually used cosine theorem implicitly. @almagest: see edit. – Quang Hoang Sep 07 '14 at 16:12
  • Sorry, I am being slow. I can see that angle A=angle C. But why is angle A=angle B? It isn't symmetrical. – almagest Sep 07 '14 at 16:21
  • 1
    You can either apply $B$ being the smallest angle, or use the fact that $C$ is now the largest angle. – Quang Hoang Sep 07 '14 at 16:23
  • Repeating with C largest gives C=B. Thanks. +1 – almagest Sep 07 '14 at 16:26
  • 1
    The "It follows that" line gives A ≤ C (not A = C). But you can easily extend A ≤ C by symmetry to A = B = C. – M.M Sep 08 '14 at 04:43
  • @MattMcNabb: $A$ is the largest angle already. – Quang Hoang Sep 08 '14 at 05:05
  • Quang Hoang's answer is by the method of Reductio ad absurdum and the conclusion of his last line follows immediately from the combination of the penultimate line and his initial supposition, and the conclusion is not so obscure as to need further explanation, as QH assumed. He also, of course, assumed that symmetry alone would be enough to declare QED, but he has later felt that he needed to make this explicit. QH is to be congratulated for such an excellent answer and my only question is how QH came to that answer in less than half an hour. Unless QH says differently I can only assume that h – jimalton Sep 16 '14 at 14:26
  • The previous comment by @jimalton was cut-off in the auto-conversion process due to length. It should end with "...I can only assume that he has encountered solutions to similar problems recently." – Willie Wong Sep 16 '14 at 15:23
  • @jimalton: Thanks for the nice words. The solution came naturally and based much on symmetry. I didn't think that it would draw that much of attention though. – Quang Hoang Sep 16 '14 at 15:42
14

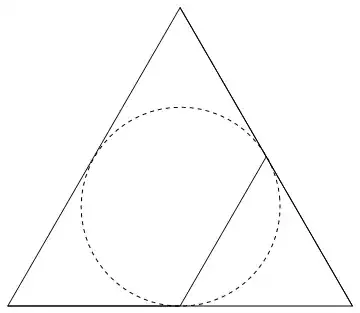
Not if DAB etc are not colinear. Consider the following:

enter image description here

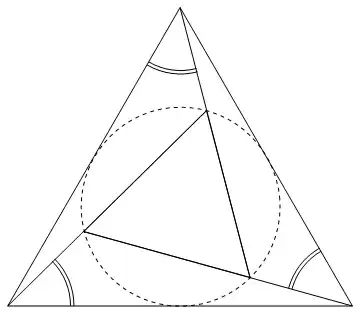
However, if they are, the centre two triangles in this give a visual proof: enter image description here

(added as visual complement to Quang Hoang's answer above)

Community
  • 1
martin
  • 8,998