1

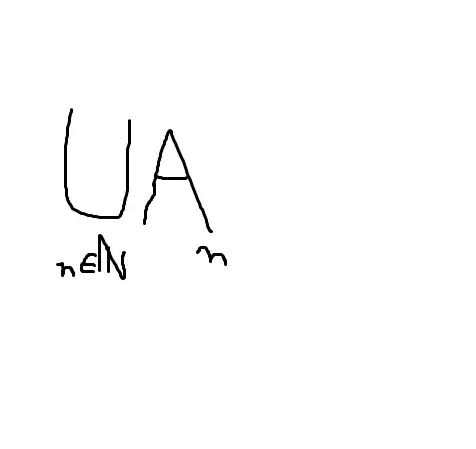
enter image description here

$$\bigcup\limits_{n\in\mathbb N} A_n$$

The book is asking me to prove that $f(\bigcup\limits_{n\in\mathbb N} A_n) = \bigcup\limits_{n\in\mathbb N} A_n$.

I'm able to prove that f(the notation above) = the notation above U A(n+1) (A(n+1) looks like An above) does that mean that f(the notation above) = the notation above? since n+1 is in N

Does this notation mean the union of the sets $A_1 \cup A_2 \cup ... \cup A_{6565656}$?

Martin Sleziak
  • 53,687
ayra
  • 19
  • Have a look here – drhab Sep 20 '14 at 14:19
  • You can write $\bigcup_{n\in\mathbb N} A_n$ to get $\bigcup_{n\in\mathbb N} A_n$ or $f(\bigcup_{n\in\mathbb N} A_n)$ to get $f(\bigcup_{n\in\mathbb N} A_n)$. – Martin Sleziak Sep 20 '14 at 14:22
  • Maybe the part of this Wikipedia article which deals with notation can clear up some thisng for you. – Martin Sleziak Sep 20 '14 at 14:23
  • You should try to edit your post to be more readable. (You have some pointers related to writing math in the above comments. I have edited the parts where it was clear what you mean.) If you want from other users also help with the part about the function $f$, you should explain what this function $f$ is or which properties of $f$ are given. – Martin Sleziak Sep 20 '14 at 14:30
  • It means the unified set containing all the elements in all the $A_n$ sets. It also means that the mouse is not very useful for writing. – barak manos Sep 20 '14 at 14:30
  • The answers below say $\bigcup \limits_{n \in \Bbb{N}}A_{n} = A_{1} \cup A_{2} \cup A_{3} \cup \ldots$, but the RHS of this inequality is, by definition, the LHS, so this doesn't help clarifying what the LHS is. Read this comment for clarification. – Git Gud Sep 20 '14 at 14:40

2 Answers2

1

Remember that the natural numbers are denoted by $\mathbb{N} = \{1,2,3,\ldots\}$.

And yes, you are correct:

$$\bigcup_{n \in \mathbb{N}} A_n = A_1 \cup A_2 \cup A_3 \cup \ldots $$

The big union symbol is just notation to express taking lots of unions more easily.

We sometimes refer to unions like $\bigcup_{n \in \mathbb{N}} A_n$ as infinite unions, because they take the union of an infinite (but countable) number of sets.

Newb
  • 17,672
  • 13
  • 67
  • 114
1

$$\bigcup_{n \in \Bbb{N}}A_{n} = A_{1} \cup A_{2} \cup A_{3} \cup \ .....$$ Next you are trying to show that $$f\left(\bigcup_{n \in \Bbb{N}}A_{n}\right) = \bigcup_{n \in \Bbb{N}}f\left(A_{n}\right)$$ These types of proofs are often done by double containment. Let $x \in f\left(\bigcup_{n \in \Bbb{N}}A_{n}\right)$. Then $f^{-1}(x) \in \bigcup_{n \in \Bbb{N}}A_{n}$, so there exists at least one $i \in \Bbb{N}$ where $f^{-1}(x) \in A_{i}$. But this means $x \in f(A_{i})$, so obviously $x \in \bigcup_{n \in \Bbb{N}}f\left(A_{n}\right)$. This establishes that $$f\left(\bigcup_{n \in \Bbb{N}}A_{n}\right) \subseteq \bigcup_{n \in \Bbb{N}}f\left(A_{n}\right).$$

Now let $y \in \bigcup_{n \in \Bbb{N}}f\left(A_{n}\right)$. Again, there has to be some $j \in \Bbb{N}$ where $y \in f(A_{j})$, which means $f^{-1}(y) \in A_{j}$. But if $f^{-1}(y) \in A_{j}$ then $f^{-1}(y) \in \bigcup_{n \in \Bbb{N}}A_{n}$. Now we apply $f$ again to both sides of this subset relation and we have $y \in f\left(\bigcup_{n \in \Bbb{N}}A_{n}\right)$. Now we have established that $$ \bigcup_{n \in \Bbb{N}}f\left(A_{n}\right) \subseteq f\left(\bigcup_{n \in \Bbb{N}}A_{n}\right).$$ By double containment, we may conclude that $$f\left(\bigcup_{n \in \Bbb{N}}A_{n}\right) = \bigcup_{n \in \Bbb{N}}f\left(A_{n}\right)$$

graydad
  • 14,077
  • I think some clarification from the OP is needed. The original post said that they want to prove: f(the notation above ) = the notation above which I understand as $f(\bigcup\limits_{n\in\mathbb N} A_n) = \bigcup\limits_{n\in\mathbb N} A_n$. (This is not true for arbitrary $f$ and $A_n$, so if this is what the OP wants, they should provide further details.) – Martin Sleziak Sep 20 '14 at 14:33
  • BTW it is worth mentioning that what you showed in your answer is a special case of this: http://math.stackexchange.com/questions/225293/show-that-bigcup-i-fa-i-f-bigcup-i-a-i – Martin Sleziak Sep 20 '14 at 14:35
  • You wrote in your proof: Then $f^{-1}(x) \in \bigcup_{n \in \Bbb{N}}A_{n}$, so there exists... But we do not know whether $f$ is bijective. If it is not bijective, the inverse function $f^{-1}$ does not exist. So if you are trying to prove this equality for arbitrary functions, you should somehow reformulated the parts using $f^{-1}$ or explain what you mean by this notation. – Martin Sleziak Sep 20 '14 at 14:38