Here's my attempt:
Let's call $C_n$ the center of the $n$th polygon for $3 \leq n$. The first part will be to calculate the smaller angle between $\overline{C_nC_{n+1}}$ and $\overline{C_{n+1}C_{n+2}}$ $4 \leq n$, which we'll call $\theta_{n+1}$ and is readily seen that is given by:
$$\theta_{n} = \frac{2\pi}{n} \left(\left\lceil\frac{n}{2}\right\rceil -1 \right)$$
So for $n=4$, $\theta_{4} = \frac{\pi}{2}$, for $n=5$, $\theta_{5} = \frac{4\pi}{5}$ and so on.
Now let's measure $\overline{C_nC_{n+1}}$:
$$|| \overline{C_nC_{n+1}}|| = \frac{s}{2}\left(tan\frac{\pi(n-2)}{2n}+tan\frac{\pi(n-1)}{2n+2}\right)$$
With this we may now compute $|| \overline{C_3C_{n}}||$, the radius and the angle of this line with respect to \overline{C_3C_4}.
Doing this analytically seems quite tiresome so I decided to program it in python. It's been a while since I programmed so I hope you don't mind the code:
from pylab import *
def theta(M): #prints angle between M-1 y M
th = ((2*pi/M)*(ceil(M/2)-1))
return th
def dcent(M): #prints distance between C_M y C_M+1
dc = (0.5*(tan(pi*(M-2)/(2*M)) + tan(pi*(M-1)/(2*M+2))))
return dc
M=1000000
r = zeros(M)
r[4] = dcent(3)
r[5] = sqrt(dcent(3)**2 + dcent(4)**2)
alpha = zeros(M)
beta = zeros(M)
phi = zeros(M)
alpha[4] = pi/2
beta[4] = arcsin(r[4]/r[5])
phi[4] = pi - alpha[4] - beta[4]
for i in arange(5,M-1,1):
alpha[i] = theta(M) - beta[i-1]
r[i+1] = sqrt(r[i]**2 + dcent(i)**2 - 2*r[i]*dcent(i)cos(alpha[i]))
beta[i] = arcsin(r[i](sin(alpha[i])/r[i+1]))
phi[i] = pi - alpha[i] - beta[i] + phi[i-1]
# print phi[i], r[i]
polar(phi[4:M-1],r[4:M-1])
show()
Where alpha and beta are the outer angles of the triangles $C_3C_nC_{n+1}$. This code yields the plot:
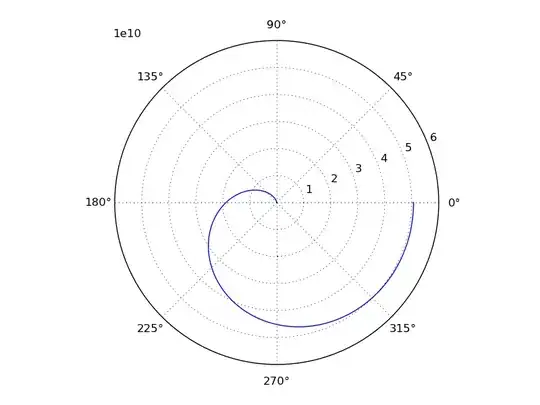
I also tried using semilog and loglog plotting, which didn't linearize the plot, so this isn't a logarithmic or power spiral. Finally, if you try the code you'll see that the spiral spiral will stop circling the origin and converge to $\phi = 0$, as it's shown in the graph.

