14

I found this in a Computer Science pseudocode context (see page 4 of this paper).

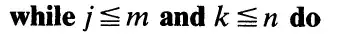
Double inequality image

8128
  • 457

4 Answers4

16

It means exactly the same as $\le$.

Clive Newstead
  • 64,925
  • 1
    Is there any particular reason for using this sign instead of $\le$ ? – 8128 Jan 11 '12 at 11:34
  • 3
    It might just be the author's preference, or the journal's convention, or just because it's an old paper and there were typographical restrictions. If you start reading even older stuff with maths in it, you'll be surprised what kooky notation and language they use (at least, it's considered kooky now). – Clive Newstead Jan 11 '12 at 11:40
  • The "<=" notation has an equals sign in it, just as "less than or equals" says equals. The "<_" notation doesn't have an equals sign. I don't know if that's correct, but it does seem plausible. – Doug Spoonwood Jan 11 '12 at 11:52
  • 3
    @Doug: It's likely that the latter evolved from the former; the meaning of $\leqq$ and $\le$ is the same, but convention has it that $\le$ is now the most commonly used. This is probably because there's no distinction that really needs to be made. This is in contrast to, say, $\simeq$ and $\cong$ in topology, which do mean different things (respectively, homotopy equivalence and homeomorphism). – Clive Newstead Jan 11 '12 at 12:02
  • 2
    ${\lower 1pt\lt}\atop\raise 1pt =$ apparently came first. http://jeff560.tripod.com/relation.html . I could not find any information on when the modern symbol "$\le$" was first used. – David Mitra Jan 11 '12 at 12:16
  • 8
    In short, $\leqq=\leq$. – Tsuyoshi Ito Jan 11 '12 at 12:44
  • You will find it in 19th century and early 20th century math books. And (it seems) some computer science guys are still using it. – GEdgar Mar 03 '18 at 12:39
5

I add a comment for the sake of completeness. As said, in general $\geqq$ means $\geq$, but in some old math texts it is possible to find the following distinction for a real vector $x$:

  • "Positive" denoted as $x > 0$: all the elements of $x$ are strictly positive;
  • "Semipositive" denoted as $ x \geq 0$: all the elements of $x$ are nonnegative but at least one of them is strictly positive;
  • "Nonnegative" denoted as $ x \geqq 0$: all the elements of $x$ are nonnegative.

In other terms, with this notation, $x \geq 0$ implies $x \neq 0$.

Tobia Marcucci
  • 729
5

It is the same old $\le$ symbol.

Mathematical notation is far from set in stone or standardised, as might appear to a beginner. Here's a sample of the variations in the inequality signs (taken from symbols-a4.pdf):

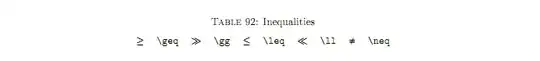
a sample of inequality signs a sample-continued

Of course, most of this is not commonly used; my guess is that they have been included only for historical purposes and for completeness.

Srivatsan
  • 26,311
0

In the given context, it means “less than or equal to,” just as “≤” means. However, it is coded as a separate character (not just a glyph variant), so it could be used for some other meaning. A symbol means whatever people make it mean.

Historically, it is a glyph variant, and it has been encoded as a character primarily for compatibility reasons, see Unicode Standard, pages 491–492.

According to the ISO 80000-2 standard, the character to be used is “≤” (U+2264).

Jukka K. Korpela
  • 205