What is the expected value of the mean of the highest $m$ numbers in a population of $N$ normally distributed random variables?

Question

Suppose that I randomly generate $N$ numbers according to the standard normal distribution, $\mathcal{N}(0,1)$. Then suppose I pick the highest $m$ numbers, $x_1\leq x_2 \leq \cdots \leq x_m$. What is the expected value of the (arithmetic) average of $x_1,\dotsc , x_m$?

Forgive me, I couldn't get my probability theory phrasing 100% accurate here. Hopefully my meaning is clear.

---

EDIT: A better attempt at proper phrasing might be,

If $a_1,\dotsc , a_N$ are real numbers and $m<N$, define $y_m(a_1,\dotsc , a_N)$ to be the average of the top $m$ values among $a_1,\ldots ,a_N$. If $X_1,\dotsc ,X_N\sim \mathcal{N}(0,1)$ are i.i.d. r.v.'s, define $Y=y_m(X_1,\dotsc ,X_N)$. What is $\mathbb{E}(Y)$?

(Would be greatful foro suggestions on how to improve the formal statement here.)

Answer 1

You can derive the result from this answer on Cross Validated.

By linearity of expectation, you just need to add the top $m$ order statistics and divide by $m$.

Answer 2

To answer this question, one must note that by generating a random number from a distribution with cumulative distribution function $F$, one is uniformly sampling the y-axis and choosing the x-axis value. Hence, we should first find the corresponding $x$-value of the partition chosen, that is $$\frac{1}{{\sqrt {2\pi } }}\int\limits_x^{ + \infty } {{e^{ - \frac{{{t^2}}}{2}}}dt} = \frac{M}{N}$$which yields $$x = \sqrt 2 {\rm{InverseErfc}}\left( {\frac{{2M}}{N}} \right)$$Now, all we have to compute is the expected value of $x$ in this range, that is $$\begin{array}{c}{\rm{Answer}} = \frac{{\frac{1}{{\sqrt {2\pi } }}\int\limits_{\sqrt 2 {\rm{InverseErfc}}\left( {\frac{{2M}}{N}} \right)}^{ + \infty } {t{e^{ - \frac{{{t^2}}}{2}}}dt} }}{{\frac{1}{{\sqrt {2\pi } }}\int\limits_{\sqrt 2 {\rm{InverseErfc}}\left( {\frac{{2M}}{N}} \right)}^{ + \infty } {{e^{ - \frac{{{t^2}}}{2}}}dt} }}\\ = \frac{N}{{\sqrt {2\pi } M}}{e^{ - \frac{{{{\left( {{\rm{InverseErfc}}\left( {\frac{{2M}}{N}} \right)} \right)}^2}}}{2}}}\end{array}$$A plot could be constructed for this problem by defining $u = \frac{N}{M}$ and noticing that $1 \le u < + \infty $ 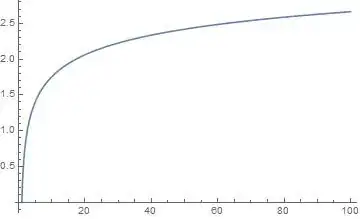Hope it helps ;)