The triangle $DEF$ circumscribes the three escribed circles of triangle $ABC$.
Prove that
$$\frac{EF}{a\,\cos A} = \frac{FD}{b\,\cos B} = \frac{DE}{c\,\cos C}$$
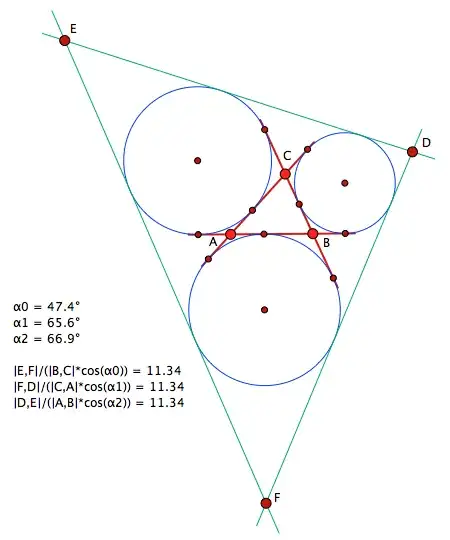
The triangle $DEF$ circumscribes the three escribed circles of triangle $ABC$.
Prove that
$$\frac{EF}{a\,\cos A} = \frac{FD}{b\,\cos B} = \frac{DE}{c\,\cos C}$$

Significant Edit to simplify the argument.
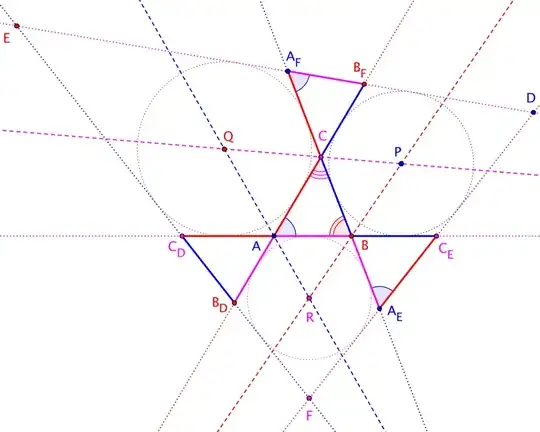
In the diagram, we note that, for instance, $\overleftrightarrow{PQ}$ bisects the angle formed by $\overleftrightarrow{AB}$ and $\overleftrightarrow{DE}$. In fact, $\overleftrightarrow{PQ}$ is a line of symmetry through elements bounded by $\overleftrightarrow{AB}$ and $\overleftrightarrow{DE}$; in particular, this line of symmetry separates $\triangle ABC$ from a mirror image, $\triangle A_F B_F C$. Likewise, $\overleftrightarrow{QR}$ and $\overleftrightarrow{RP}$ give us mirror images $\triangle AB_DC_D$ and $\triangle A_EBC_E$.
As a result, $\triangle DA_EA_F$ is an isosceles triangle with base angles of size $A$. This, along with corresponding observations about $\triangle EB_FB_D$ and $\triangle FC_DC_E$, tells us $$\angle D = 180° - 2\;\angle A \qquad \angle E = 180° - 2\;\angle B \qquad \angle F = 180° - 2\;\angle C $$
Now, turning our attention to $\triangle DEF$, we invoke the Law of Sines: $$\frac{|\overline{EF}|}{\sin D} = \frac{|\overline{FD}|}{\sin E} = \frac{|\overline{DE}|}{\sin F}$$ Therefore, as $\sin(180°-\theta) = \sin\theta$, $$\frac{|\overline{EF}|}{\sin 2A} = \frac{|\overline{FD}|}{\sin 2B} = \frac{|\overline{DE}|}{\sin 2C}$$ and, as $\sin 2\theta = 2\sin\theta\cos\theta$, $$\frac{|\overline{EF}|}{2\sin A \cos A} = \frac{|\overline{FD}|}{2\sin B \cos B} = \frac{|\overline{DE}|}{2\sin C\cos C} \tag{$\star$}$$
Recall that the Law of Sines for $\triangle ABC$ —say, with circumdiameter $m$— implies $$a = m \sin A \qquad b = m \sin B \qquad c = m \sin C$$ This allow us to write $(\star)$ as $$\frac{m\;|\overline{EF}|}{2a\;\cos A} = \frac{m\;|\overline{FD}|}{2b\;\cos B} = \frac{m\;|\overline{DE}|}{2c\;\cos C}$$
Dividing-through by $m/2$ gives the result. $\square$
I think just because $PQ $ is not extended backwards you are not seeing a situation of symmetry between direct and inverse tangents. I have relabeled for convenience, extended the direct tangents and line of centers to be concurrent at $F$ enabling comparison of angles.