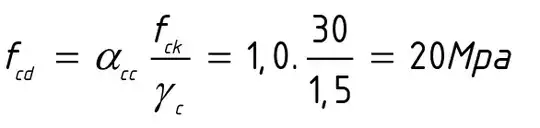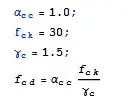How to show formula and substitute variable values?

Question

I'm looking for an easy way to make a 'dynamic' paper for some engineering calculations (I'm talking about hundreds of pages with lots of different formulas). The problem is hard to describe so I'll show a picture - this is a sample of the expected output output

Formula -> Values of the Variables -> Final Result [Dimension]

So I typed the following

input

And the output is just 20. (Without showing formula).

I saw that HoldForm can print the formula and ReleaseHold can print the final output. But I can't find a way to show the intermediate result - where all variables are substituted by their values.

Subscript[α, c*c] = 1.; 
Subscript[f, c*k] = 30; 
Subscript[γ, c] = 1.5; 
Subscript[f, c*d] = Subscript[α, c*c]*(Subscript[f, c*k]/Subscript[γ, c])

Please type out your code, it makes it easier for people to help you — Peter Roberge, Nov 21 '15 at 18:12
Posted it... I'm not sure how this looks any better / more readable than the image. — user5589484, Nov 21 '15 at 18:20
Welcome to Mathematica.SE! I suggest the following: 1) As you receive help, try to give it too, by answering questions in your area of expertise. 2) Take the tour! 3) When you see good questions and answers, vote them up by clicking the gray triangles, because the credibility of the system is based on the reputation gained by users sharing their knowledge. Also, please remember to accept the answer, if any, that solves your problem, by clicking the checkmark sign! — Michael E2, Nov 21 '15 at 18:27
You may find this this meta Q&A helpful in formatting your code in a more readable manner. — Michael E2, Nov 21 '15 at 18:28

Edmund · Answer 1 · 2015-11-24T18:53:43.807

You may use HoldForm along with Inactivate to produce the results you seek.

First I suggest changing the input of your subscripts so they are not multiplying the indices. You can do this by inserting Esc,Esc in between the indices to have them not multiply. The full form is then Subscript[f, c, d].

Moving on:

ClearAll[showSubstitution];
Attributes[showSubstitution] = {HoldAll};
showSubstitution[sym_, formula_] := 
 HoldForm[sym] == HoldForm[formula] == 
  Inactivate[formula, Except[Subscript]] == formula

showSubstitution takes the symbol of the formula ($f_{c,d}$) and the formula ($\frac{\alpha _{c,c} f_{c,k}}{\gamma _c}$) and displays the substitution steps to the result. It does loose the fraction formatting on the substitution as the denominator is taken to be the value to power -1.

Subscript[f, c, k] = 1;
Subscript[α, c, c] = 30;
Subscript[γ, c] = 1.5;

Subscript[f, c, d] = (Subscript[f, c, k]*Subscript[\[Alpha], c, c])/Subscript[\[Gamma], c]

showSubstitution[Subscript[f, c, d], 
 (Subscript[f, c, k] Subscript[α, c, c])/Subscript[γ, c]]

$\gamma _c=1.5;$

$\alpha _{c,c}=30;$

$f_{c,k}=1;$

$f_{c,d}=\frac{\alpha _{c,c} f_{c,k}}{\gamma _c};$

$\text{showSubstitution}\left(f_{c,d},\frac{\alpha _{c,c} f_{c,k}}{\gamma _c}\right)$

$f_{c,d}=\frac{f_{c,k} \alpha _{c,c}}{\gamma _c}=1*30*1.5{}^{\wedge}(-1)=20.$

HoldForm (and HoldAll on the function attributes) keeps the symbols from being replaced with their values. Inactivate allows the values to be substituted in but prevents the functions from executing. Subscript is Excepted so the symbols with subscripts will resolve.

Hope this helps.

score 0 · Answer 2 · edited Nov 22 '15 at 15:04

0

You can create rules which include HoldForm:

r = {Subscript[α, c c] -> HoldForm[1.0],
Subscript[f, c k] -> HoldForm[30],
Subscript[γ, c] -> HoldForm[1.5]}

Then use the rules:

Subscript[f, c d] = Subscript[α, c c] 
Subscript[f, c k]/Subscript[γ, c] /. r

Will give you:

1. 30 / 1.5

edited Nov 22 '15 at 15:04

bbgodfrey

61,439
17
89
156

answered Nov 21 '15 at 18:41

Peter Roberge

2,357
11
19

Is there an easier way? I got the idea but it's too much work for only a single formula and there will be a lot more. And when I have to chain it with the next formulas (use the results from this) - it's getting messy. (I tried to Append[r, Fcd -> HoldForm[Fcd]] and the list looks the opposite of what it should look - Instead of Fcd->20 it's 20->Fcd). – user5589484 Nov 21 '15 at 20:00

How to show formula and substitute variable values?

2 Answers2

Linked