I get a rectangle and a circle like following:
The Harmonic Tool of CorelDraw can transition the rectangle to circle smoothly like this
So how can I get the transitional images from the given rectangle to the given circle.There is a similar topic of me.How to resample a list of Images,If we use the method of @shrx we cannot get result that I want
With[{img3d = Image3D[imgs]},
ImageResize[img3d, ImageDimensions[img3d]*{1, 1, 100},
Resampling -> "Linear"]]
Not exactly what you are asking for but the specific case of circle->square can be done mathematically as both are special cases of hyperellipses:
Manipulate[
Show[ParametricPlot[ {#[[1]] x, #[[2]] (1 -
x^(2^n))^(1/(2^n))} , {x, 0, 1}, AspectRatio -> 1] & /@ {{1,
1}, {-1, 1}, {-1, -1}, {1, -1}}, Axes -> False,
PlotRange -> {{-1, 1}, {-1, 1}}] , {{n, 1}, 1, 8}]
as another more general approach if you can get your graphics into line form with the same number of points in each you can do a simple interpolation. Example:
n = 160; (*must be multiple of 8*)
c = Table[ {-Cos[2 Pi x/n + Pi/4] , -Sin[2 Pi x/n + Pi/4]}, {x, 0, n}];
r = Join[
Table[ {8 x/n , -1}, {x, -n/8, n/8 - 1}],
Table[ {1, 8 x/n}, {x, -n/8, n/8 - 1}],
Table[ {8 x/n, 1}, {x, n/8, -n/8 + 1, -1}],
Table[ {-1, 8 x/n}, {x, n/8, -n/8, -1}]
];
Manipulate[Graphics[Line[w r + (1 - w ) c]], {w, 0, 1}]
In your particular case with Rectangle -> Circle you can simply use RoundingRadius:
GraphicsRow@Table[Graphics@Rectangle[{0, 0}, RoundingRadius -> r], {r, 0, .5, .1}]
A general image-based method was discussed here.
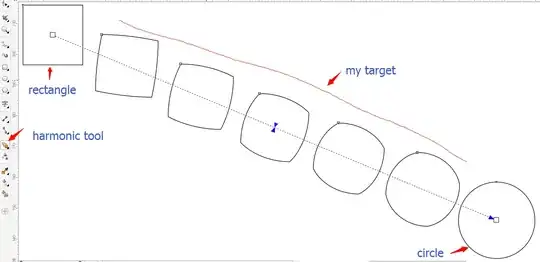
Here is a method that uses some very basic image processing to work for fairly general figures (any convex black-and-white shape, I believe). First, I get the images:
In[1]:= rect = Import["https://i.stack.imgur.com/mkv8a.png"];
circ = Import["https://i.stack.imgur.com/Gy44u.png"];
Now, I use ImageValuePositions and Binarize to find the points of the drawing (note that Binarize flips black and white), and MeshPrimitives and ConvexHullMesh to eliminate redundant points introduced but the thickness of the lines and to put the points in a sensible order:
centered[p_] := Transpose[Transpose[p] - Mean@p];
lines[p_] := MeshPrimitives[ConvexHullMesh[p], 1];
points[img_] :=
With[{p = ImageValuePositions[Binarize@img, White]},
centered@DeleteDuplicates[Flatten[lines[p] /. Line -> Identity, 1]]];
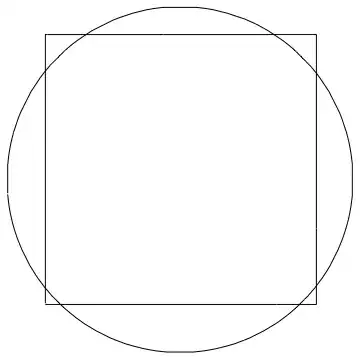
In[3]:= startPoints = points@circ;
endPoints = points@rect;
Now seems like a good time to check that things look right:
In[4]:= Graphics[{Line[startPoints], Line[endPoints]}]
Out[4]=
Next, I want to linearly interpolate between these sets of points, which means setting up correspondences between the two sets of points. I do this using Nearest and GroupBy:
correspondance[start_, end_] :=
With[{
sorted = SortBy[{start, end}, Length],
dir = If[Length[start] < Length[end], Forward, Backward]
},
{dir, GroupBy[Last@sorted, Nearest@First@sorted]}];
I pick the direction because I want to make sure that if I have more points in one list, the many-to-one mapping is done properly by GroupBy. Now it's just a matter of turning this into a linear interpolation:
paired[corr_Association] := Transpose[
Flatten[KeyValueMap[Tuples@*List, corr], 1]];
order[Backward, paired_] := Reverse@paired
order[Forward, paired_] := paired;
lerp[{dir : (Forward | Backward), corr_}] :=
Replace[order[dir, paired@corr],
{start_, end_} :>
With[{diff = end - start},
Function[t, start + t*diff]]];
Now we just plug everything in:
In[8]:= l = lerp@correspondance[startPoints, endPoints];
Here's an animation of Table[Graphics@Line[l[t]], {t, 0, 1, 0.05}]:
