2

A couple of years ago I asked a question about solving n-body systems with NDSolve and detecting collisions with WhenEvent. I received an excellent answer, but unfortunately that code does not work anymore in Mathematica 10.2.0.

In particular, in v9 the integration continued after the collision (which occurs at t=2.39343) and properly updated the modified masses and velocities of particles, as can be seen in the resulting trajectories plot:

ParametricPlot3D[Evaluate[#@t & /@ pos], {t, 2.25, 2.43}, 
 PlotRange -> All, ImageSize -> 500, PlotPoints -> 500, 
 MaxRecursion -> 15, Boxed -> False, Axes -> False]

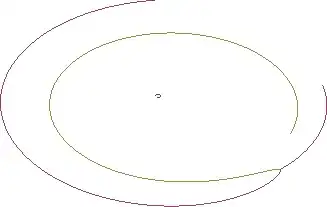
parametric plot from mma 9

In Mathematica 10, however, after the collision, the system falls apart and NDSolve can't produce sensible trajectories anymore - the parametric plot now looks like this:

enter image description here

How to fix the code in the linked answer for Mathematica 10 so that it will properly detect the collisions and update the masses and velocities of particles?

Community
  • 1
shrx
  • 7,807
  • 2
  • 22
  • 55
  • The first time I run the code, I get an error. It seems pids[[1]] is being evaluated before pids is defined. If I run the code a second time, it goes through without an error. The plot I get is the same as you V9 plot (V10.2, Mac OS): http://i.stack.imgur.com/J0oIL.png – Michael E2 Nov 24 '15 at 14:44
  • @MichaelE2 Interesting, I have the same specs. It happens on a fresh kernel. I get the errors too, but it doesn't affect the output. – shrx Nov 24 '15 at 14:56
  • 1
    No difference on a fresh kernel for me. If I put a random initialization, say, pids = {1, 2};, before whenevnt, it works fine. If I wrap the second argument of WhenEvent in Module[{pids},...], the error refers to pids$[[1]], which shows that NDSolve is inspecting the held code, since pids$ does not have a module number at the end. The error then gives a stiffness/singularity warning and integration stops at the collision. In that case, I get your V10 graph. Try the initialization dodge. See if it works. – Michael E2 Nov 24 '15 at 15:05
  • 2
    My guess is that when the part error on pids[[1]] happens, NDSolve decides to ignore the event. Seems like a bug to me. At the least, there ought to be a message warning the user that there was an error in the event and that the event is being ignored (assuming it is ignored and not merely misfiring). – Michael E2 Nov 24 '15 at 15:11
  • The error occurs in the NDSolve`ProcessEquations stage, which is not surprising. – Michael E2 Nov 24 '15 at 15:31
  • strange: I just tried this on my Windows 7, 64bit box with Mathematica 10.2 and 10.3 and while I see the same errors, for me the event is working as intended, even on first try... – Albert Retey Nov 24 '15 at 15:35
  • Very strange: after a computer restart, it's working for me too now if I perform the pid initialization trick like @MichaelE2 suggested. If I dont, I get the same (wrong) result as shown in the question. – shrx Nov 24 '15 at 17:12
  • Sometimes, when I execute the code in Mathematica 10, I get the error: NDSolve::ndsz: At t == 2.3934322946201605, step size is effectively zero; singularity or stiff system suspected. >> and integration stops there. Collision is still detected, but I get garbage trajectories as shown in OP. – shrx Nov 24 '15 at 18:08
  • The "garbage trajectory" comes from extrapolation beyond t == 2.3934322946201605 -- use the plotting domain {t, 2.25, 2.3934322946201605`} and you'll see something reasonable. – Michael E2 Nov 24 '15 at 19:24
  • @MichaelE2 I also need the trajectories beyond the collision point (not extrapolated but calculated with the new masses and velocities specified within WhenEvent). – shrx Nov 24 '15 at 19:26
  • I realize that, but when the integration stops at 2.39, it stops and the trajectory beyond the collision is not computed. (I just meant to point out that the straight line is itself not an error in Mathematica, but the result of the collision event malfunctioning.) – Michael E2 Nov 24 '15 at 19:29
  • @MichaelE2 is it possible to continue the integration with new parameters? – shrx Nov 24 '15 at 19:30
  • It seems the velocities go to infinity at the singularity. Not surprising, but restarting the integration is not so straightforward. The initializing pids does not always work, then? (It sounded that way, but I wasn't sure.) – Michael E2 Nov 24 '15 at 19:37

0 Answers0