Substitute tangents plane in a function

Question

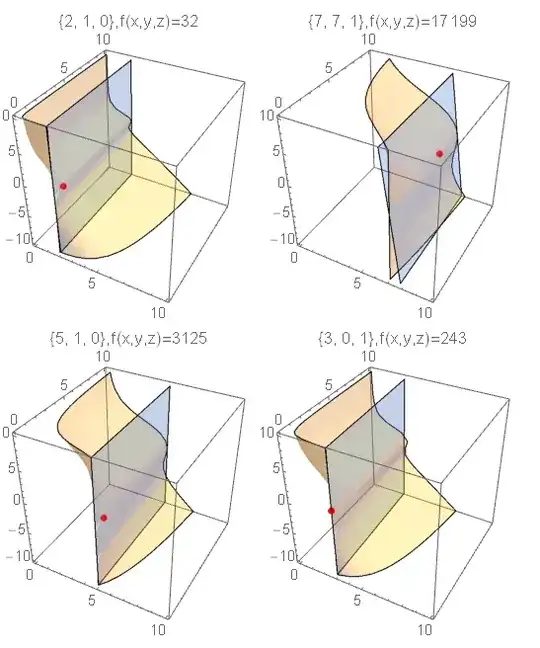
Let f:= x^5+x^2*y*z^2+z^3*x*y; and let S= {{2,1,0},{7,7,1},{5,1,0},{3,0,1}} be a set of points . I need to calculate the tangent planes at each point of S and then substitute the tangent planes in f .

I have tried to compute the tangents as below but to substitute the tangent planes in f , I couldn't do that.

f := x^5 + x^2*y*z^2 + z^3*x*y;
diff[var_, point_] := 
 D[f, var] /. {x -> point[[1]], y -> point[[2]], z -> point[[3]]}
tangent[point_] := (x - point[[1]]) diff[x, 
    point] + (y - point[[2]]) diff[y, point] + (z - point[[3]]) diff[
    z, point] + (f /. {x -> point[[1]], y -> point[[2]], 
     z -> point[[3]]})
m = {{2, 1, 0}, {7, 7, 1}, {5, 1, 0}, {3, 0, 1}};
tangent /@ m // FullSimplify
(* {16 (-8 + 5 x), 7 (-9828 + 1730 x + 8 y + 119 z), 
 3125 (-4 + x), 405 x + 12 (-81 + y)} *)

Your code looks sound, it calculates the equation for the tangent hyperplanes. But what do you mean by "substitute the tangent planes"? — Jason B., Nov 25 '15 at 11:56

score 3 · Answer 1 · answered Nov 25 '15 at 13:10

This seems like a duplicate. If so I am happy to delete this. You can exploit gradient (Grad) and then define tangent plane based on normal and visualize using ContourPlot3D:

Setup:

pts = {{2, 1, 0}, {7, 7, 1}, {5, 1, 0}, {3, 0, 1}}
f[x_, y_, z_] := x^5 + x^2*y*z^2 + z^3*x*y;
g[u_, v_, w_] := 
 Grad[f[x, y, z], {x, y, z}] /. {x -> u, y -> v, z -> w}
v = f @@@ pts

Visualization:

Partition[
  MapThread[
   Show[ContourPlot3D[{f[x, y, z] == #1, 
       Evaluate[({x, y, z} - #2).(g @@ #2) == 0]}, {x, 0, 10}, {y, 0, 
       10}, {z, -10, 10}, Mesh -> None, ContourStyle -> Opacity[0.3]],
      Graphics3D[{Red, PointSize[0.03], Point@#2}], 
     PlotLabel -> Row[{#2, ",f(x,y,z)=", #1}]] &, {v, pts}], 
  2] // Grid

Dr. belisarius · Answer 2 · 2015-11-25T13:57:51.587

I find this way particularly clear:

tan1[fun_, vars_, pt_] := Module[{u = Unique[vars]},
                          Grad[fun@u, u].(vars - u) + fun@u /. Thread[u -> pt] ]

m = {{2, 1, 0}, {7, 7, 1}, {5, 1, 0}, {3, 0, 1}};
k[{x_, y_, z_}] := x^5 + x^2*y*z^2 + z^3*x*y;

ContourPlot3D[{
    k[{x, y, z}] == k@#, tan1[k, {x, y, z}, #] == k@#},
    {x, 0, 10}, {y, 0, 10}, {z, -10, 10}, Mesh -> None, 
   ContourStyle -> Opacity[0.3], Evaluated -> True] & /@ m

Mathematica graphics

Substitute tangents plane in a function

2 Answers2