Wiggly and imprecise animated gif output

Question

Trying to make animated gif of zooming into famous Ford circles. With the code

visibleQ[lh_, hr_, c_, k_] := Which[
  lh >= 1/(2 k), If[2 c k^2 <= 1 && lh^2 < c (1 - c k^2), True, False],
  hr >= 1/(2 k), If[2 c k^2 <= 1 && hr^2 < c (1 - c k^2), True, False],
  True, True]
t = {}
With[{center = 1/π, s = 1.04, start = 60},
 Module[{d = s^start},
  For[maxz = start, maxz < 300, maxz++; d *= s,
   With[{a = center - 2/3/d, b = center + 2/3/d, c = 2/3/d, e = -1/120/d},
    AppendTo[t,
     Graphics[
      {
       Line[{{-1, 0}, {2, 0}}],
       Table[
        Map[
         Circle[{#/k, 1/(2 k^2)}, 1/(2 k^2)] &,
         Select[Range[k], visibleQ[a k - #, # - b k, c, k] && CoprimeQ[#, k] &]
        ],
        {k, 12 Sqrt[3 d/2]}
       ]
      },
      ImageSize -> 500, PlotRange -> {{a, b}, {e, c}}
     ]
    ]
   ]
  ]
 ]
]
Export["..\\Desktop\\ford240.gif", t]

(which I adapted from a Wolfram demonstration and optimized a bit) I get this:

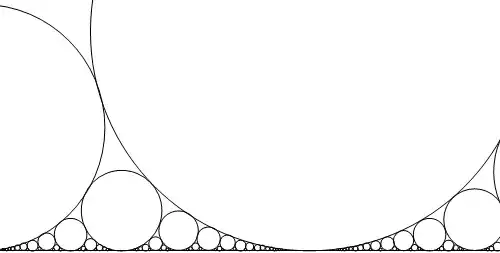
As you see the circles tremble unpleasantly, and occasionally intersect each other, although according to the formulæ they must always touch only.

How can this be improved?

Searching for similar questions I only found How to avoid the wiggly text on Ticks and Labels when rotating 3D objects but that one is about text and I could not figure out whether it might be useful in any way here.

There is another problem too. It concerns mathematics rather than Mathematica, but still let me ask about it here. By monitoring maxz I found out that each next frame renders more slowly than the previous - which is of course understandable as it requires working with larger and larger ranges of k. But on the other hand the number of circles in each frame is roughly the same, so in principle there must be a way to program it so that every frame takes roughly the same amount of time. Can it be done?

Update

Using the suggestion by J. M. I switched to Farey sequences. This allowed to remove coprimeness check, but strangely enough became even slower. I don't know why but now rasterization takes more time.

visibleQ[a_, b_, c_, x_] := 
 With[{r = 1/(2 Denominator[x]^2)}, Which[
   x <= a - r, If[r c <= 1 && (a - x)^2 < c (2/r - c), True, False],
   x >= b + r, If[r c <= 1 && (x - b)^2 < c (2/r - c), True, False],
   True, True]
  ]
tocircle[x_] := With[{r = 1/(2 Denominator[x]^2)}, Circle[{x, r}, r]]
With[{center = 1/π, zoomstep = 1.04, start = 60, size = 504},
 Module[{d = zoomstep^start},
  For[count = start; t = {}, count < 300, count++; d *= zoomstep,
   With[{left = center - 2/3/d, right = center + 2/3/d, height = 2/3/d, bottom = -1/120/d},
    l = Select[FareySequence[Floor[Sqrt[3 size d]/2]], visibleQ[left, right, height, #] &];
    AppendTo[t,
     Rasterize[
      Graphics[
       {Line[{{-1, 0}, {2, 0}}], Map[tocircle, l]},
       ImageSize -> size, PlotRange -> {{left, right}, {bottom, height}}
      ]
     ]
    ]
   ]
  ]
 ]
]

And there is hardly any improvement on accuracy of the plot.

Update 2

Still could not figure out what's wrong with Farey sequences, so I abandoned them and improved instead the visibility check. It is now reasonably quick, reached 725 frames in less than an hour. So the second question seems to be settled, but the first one (about wiggling and crossings) remains.

Here is the new code - less readable I'm afraid.

frames = {};
With[{center = 1/π, zoomstep = 1.04, start = 60, size = 504},
 Module[{d = 3 zoomstep^start, maxden = 0, rats = {}, outrats, inrats, newrats, den},
  Do[
   With[{left = center - 2/d, right = center + 2/d, height = 2/d, bottom = -1/40/d},
    outrats = 
     Select[Select[rats, 2 Last[#]^2 height <= 1 &], 
      With[{oden = Last[#], pm = Sqrt[height (1 - Last[#]^2 height)]},
         left oden - pm < First[#] < right oden + pm] &];
    inrats = 
     Select[Select[rats, 2 Last[#]^2 height > 1 &], 
      With[{iden = Last[#], pm = 1/(2 Last[#])}, 
        left iden - pm < First[#] < right iden + pm] &];
    For[den = maxden + 1; newrats = {}, den^2 <= d size, den++,
     newrats = 
      Union[newrats, 
       Map[{#, den} &, 
        Select[Range[Ceiling[left den - 1/(2 den)], 
          Floor[right den + 1/(2 den)]], CoprimeQ[#, den] &]]]
     ];
    rats = Union[outrats, inrats, newrats];
    maxden = Max[Map[Last, rats]];
    d *= zoomstep;
    AppendTo[frames,
     Graphics[
      {
       Line[{{0, 0}, {1, 0}}],
       Map[With[{r = 1/(2 Last[#]^2)}, Circle[{Divide @@ #, r}, r]] &, rats]
      },
      ImageSize -> size, PlotRange -> {{left, right}, {bottom, height}}
      ]
     ]
    ],
   900
   ]
  ]
 ]

Update 3

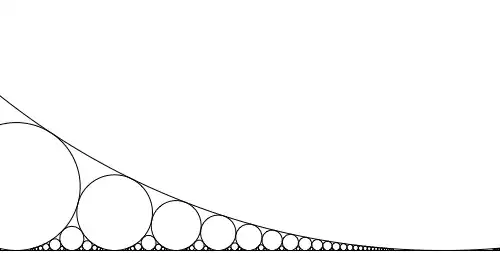
As requested by Alexey Popkov I've tried to isolate one simple case of the phenomenon. With wiggling I don't even realize how to proceed, however with circle crossings there is a very clear case: I've tried

Manipulate[
 Show[Graphics[{Circle[{0, 1/2}, 1/2], Circle[{1/q, 1/(2 q^2)}, 1/(2 q^2)]}], 
  PlotRange -> {{1/q - 1/(2 q^2), 1/q + 1/(2 q^2)}, {0, 1/q^2}}
 ],
 {q, 1, 100, 1}
]

and discovered that already starting from q=4 the crossing is clearly visible. Here is a snapshot with q=21, together with a calculation showing that these circles must intersect in only one point

Answer 1

Try calculating your own circles. (This puts the computation in the CPU with 64-bit floats instead of, I assume, in the GPU with 16/24/32-bit floats, depending on the processor and implementation.) The minimum number of circle points (12 below) might need adjusting to the clarity & resolution of the display device.

circle[pt_, r_, scale_] := 
  Line@ Append[#, First[#]] &@ CirclePoints[N@pt, N@r, Ceiling[Max[12, 60*2 Pi r/scale]]];

Or pre-V10.1:

circle[pt_, r_, scale_] := 
  With[{npts = Ceiling[Max[12, 2 Pi r/scale]]}, 
   Line@ Transpose[
     pt + r Through[{Cos, Sin}[Rescale[N@Range[npts], {1, npts}, {0., 2. Pi}]]]]
   ];

Then replace Circle[..] & with

circle[{#/k, 1/(2 k^2)}, 1/(2 k^2), Abs[c - e]] &