I need to plot the following singular double integration $u(x,t)$ for $t=0, t=0.2, t=0.4, t=1$ and $t=2$ in one figure as a line. That is, I need $u$-coordinate vertically and $x$-coordinate horizontally.
where $f(y)= \exp(-(y-4.68)^2/0.4)$. Due to singularities, I cannot plot $u(x,t)$ for $x=0..15$. I checked the NIntegrate Integration Strategies website. But, I could not manage.
t = 0.2;
m = 0.2;
f[y_] := Exp[-(y - 4.68)^2/0.4]
u[x_, t_, m_] :=
NIntegrate[
f[y] (2. Sin[(x^2 + y^2)/(8. (t - r)) + \[Pi]/4] Cos[( x y)/(
4. (t - r))]) (Exp[-(x + y)^2/(8. r)] (x + y - 4. m r)/(
4. \[Pi] r Sqrt[r (t - r)]) + (m^2 Sqrt[2.])/Sqrt[\[Pi] (t - r)]
Exp[m (x + y) + 2. m^2 r] Erfc[(x + y + 4. m r)/(
2. Sqrt[2 r])]), {y, 0., Infinity}, {r, 0, t}]

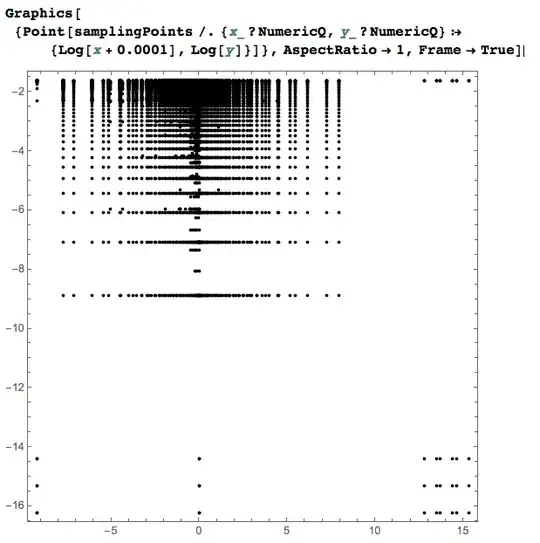
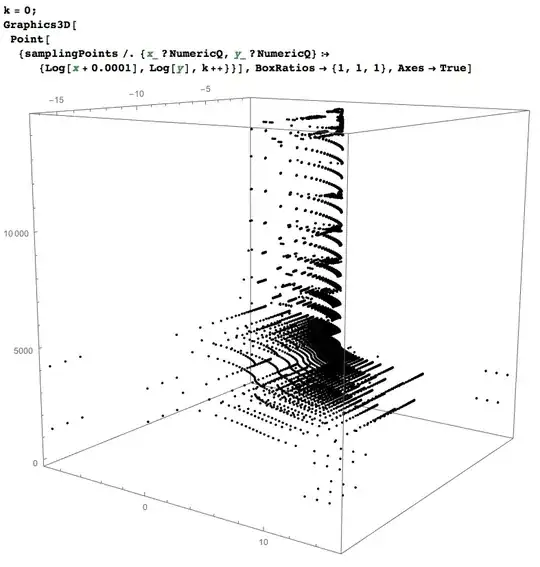
Table[{t, x, u[x, t, 0.2]}, {t, {0, 0.2, 0.4, 1, 2}}, {x, 0, 15, 0.1}]overnight and after 10 hours it was still not finished. (UsingPrecisionGoal->3.) – Anton Antonov Nov 29 '15 at 15:46