Magnifying Glass on a Plot

Question

Although there is a trick in TEX magnifying glass but I want to know is there any function to magnifying glass on a plot with Mathematica?

For example for a function as Sin[x] and at x=Pi/6

Below, this is just a picture desired from the cited site. the image got huge unfortunately I don't know how can I change the size of an image here!

Answer 1

There are built-in magnifying glasses. However, spontaneously I don't know how to invoke one directly for a Plot. Therefore I'm going to demonstrate one way that converts the Plot Graphics object into an Image:

Image@Plot[Sin[x], {x, 0, 4}]
FrontEndExecute[FrontEnd`Select2DTool["GetRectangleImageSelection"]]

---

The image ribbon itself is

FileNameJoin[{$InstallationDirectory, "SystemFiles", "FrontEnd", 
  "SystemResources", "AttachedImage2D.nb"}]

---

One can use, for example, Tooltip to get a magnified Plot at the current MousePosition.

Plot[Tooltip[Sin[x], 
  Dynamic@Plot[
    Sin[xx], {xx, First@MousePosition["Graphics", {0, 0}] - 0.1, 
     First@MousePosition["Graphics", {0, 0}] + 0.1}, Frame -> True, 
    Axes -> False, PlotRange -> All, ImageSize -> 400, 
    Background -> None], TooltipDelay -> 0, 
  TooltipStyle -> {Background -> None, CellFrameColor -> None}], {x, 0, 5}, ImageSize -> 700]

Or use the Get Coordinates tool, which gets activated by selecting the graphics and pressing ..

Plot[Sin[x], {x, 0, 5}, 
 CoordinatesToolOptions -> {"DisplayFunction" -> 
    Function[pt, 
     Plot[Sin[x], {x, pt[[1]] - 0.1, pt[[1]] + 0.1}, 
      Background -> White]]}, ImageSize -> 700]

Answer 2

Insetting a magnified part of the original Plot

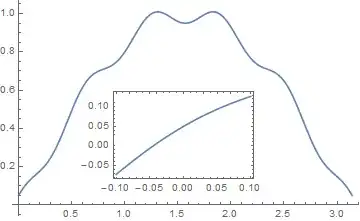
A) by adding a new Plot of the specified range

xPos = Pi/6;
range = 0.2;
f = Sin;
xyMinMax = {{xPos - range, xPos + range}, 
  {f[xPos] - range*GoldenRatio^-1, f[xPos] + range*GoldenRatio^-1}};

Plot[f[x], {x, 0, 5}, 
 Epilog -> {Transparent, EdgeForm[Thick], 
   Rectangle[Sequence @@ Transpose[xyMinMax]], 
   Inset[Plot[f[x], {x, xPos - range, xPos + range}, Frame -> True, 
     Axes -> False, PlotRange -> xyMinMax, ImageSize -> 270], {4., 0.5}]}, ImageSize -> 700]

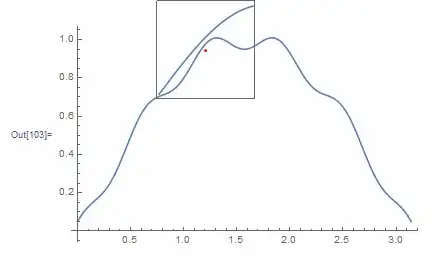
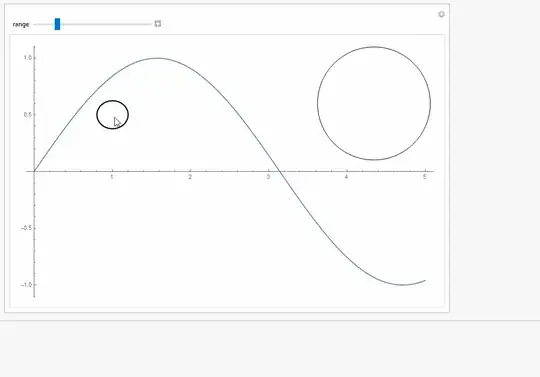
B) by adding a new Plot within a Circle

mf = RegionMember[Disk[{xPos, f[xPos]}, {range, range/GoldenRatio}]]

Show[{Graphics@Circle[{xPos, f[xPos]}, {range, range/GoldenRatio}], 
  Plot[f[x], {x, xPos - range, xPos + range}] /. 
   Graphics[{{{}, {}, {formating__, line_Line}}}, stuff___] :> 
    Graphics[{{{}, {}, {formating, 
        Line[Pick[line[[1]], mf[line[[1]]]]]}}}, stuff]}, 
 PlotRange -> All, ImageSize -> 200, AspectRatio -> 1, 
 AxesOrigin -> {0, 0}]

Plot[f[x], {x, 0, 5}, 
 Epilog -> {Transparent, EdgeForm[Thick], 
   Disk[{xPos, f[xPos]}, {range, range/GoldenRatio}], 
   Inset[%, {4.1, 0.5}]}, ImageSize -> 700]

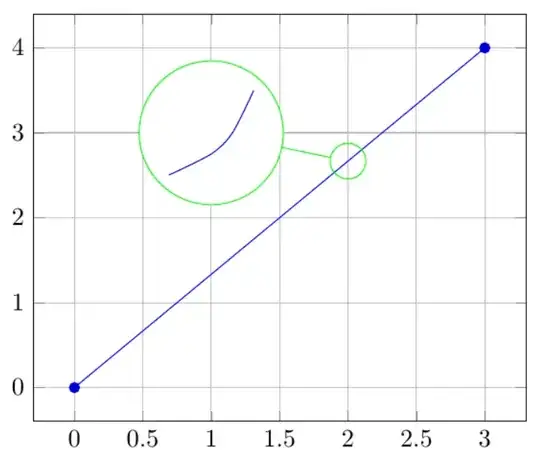
C) by adding the Line segments within a Circle of the original Plot

Show[{Graphics[{Green, 
    Circle[{xPos, f[xPos]}, {range, range/GoldenRatio}]}],
  Plot[f[x], {x, 0, 5}] /. 
   Graphics[{{{}, {}, {formating__, line_Line}}}, stuff___] :> 
    Graphics[{{{}, {}, {formating, 
        Line[Pick[line[[1]], mf[line[[1]]]]]}}}, stuff]}, 
 PlotRange -> All, ImageSize -> 200, AspectRatio -> 1]

Plot[f[x], {x, 0, 5}, 
 Epilog -> {Green, Line[{{xPos + range, f[xPos]}, {3.38, 0.5}}], 
   Transparent, EdgeForm[Green], 
   Disk[{xPos, f[xPos]}, {range, range/GoldenRatio}], 
   Inset[%, {4.1, 0.5}]}, ImageSize -> 700]

Answer 3

This is an interactive zoom that you can use in CDF or notebook. It plots a small x-range around the MousePosition as it moves around the main plot and Insets that smaller plot into the main plot.

f[x_] := Sin[x] + 0.05 Cos[10 x]


Plot[f[x], {x, 0, π},
 Epilog -> {
   Dynamic[
    With[{xpos = First@MousePosition[{"Graphics", Plot}, {π/2, 0}]},
     Inset[
      Plot[f[x], {x, xpos - 0.1, xpos + 0.1},
       Frame -> True, Axes -> False, ImageSize -> Small
       ],
      {0.6, 0.05}, ImageScaled[{0, 0}]
      ]
     ]]
   }
 ]

Hope this helps.

Answer 4

Why not use the mouse cursor? This version shows the zooming frame when CTRL is pressed.

f[x_] := Sin[x] + 0.05 Cos[10 x];

DynamicModule[{p},
 Dynamic@MouseAppearance[
   Plot[f[x], {x, 0, Pi}],
   If[CurrentValue@"ControlKey", 
    p = First@MousePosition["Graphics", {0, 0}]; 
    Plot[f[x], {x, p - 0.1, p + 0.1}, Frame -> True, 
     FrameTicks -> None, AspectRatio -> 1, Axes -> False, 
     ImageSize -> 100, Epilog -> {Red, Point@Scaled@{.5, .5}}], 
    Automatic, Automatic]]]

Answer 5

Here is one way, how you can make a Manipulate to dynamically change the magnified area and then use Setting to get the Plot together with the magnification parts as a static graphics object to be exported.

f = Sin;

Manipulate[
 Plot[f[x], {x, 0, 5}, 
  Epilog -> {Transparent, EdgeForm[Thick], 
    Disk[pos, {range, range/GoldenRatio}], 
    Inset[Show[{Graphics@Circle[pos, {range, range/GoldenRatio}], 
       Plot[f[x], {x, xPos - range, xPos + range}, 
        RegionFunction -> 
         Function[{x, y}, 
          RegionMember[
           Disk[pos, {range, range/GoldenRatio}], {x, y}]]]}, 
      PlotRange -> All, ImageSize -> 200, AspectRatio -> 1, 
      AxesOrigin -> {0, 0}], {4.35, 0.6}]}, 
  ImageSize -> 700], {{range, 0.2}, 0.01, 1}, {{xPos, 1}, None}, {mf, 
  None},
 {{pos, {1, 0.5}}, Locator, Appearance -> None, 
  TrackingFunction -> (pos = #; xPos = pos[[1]]; &)}]