Strange eigenvector behaviour for matrix with large numerical values

Question

I'm trying to compute the eigenvectors of a matrix with large numerical values

$$ \left( \begin{array}{ccccc} 0 & 1.\times 10^{18} & 100 \text{X} & 0 & 1.\times 10^{11} \text{X} \\ 1.\times 10^{18} & 0 & 0 & 0 & 0 \\ 100 \text{X} & 0 & 1.\times 10^{22} & 1.\times 10^{18} & 0 \\ 0 & 0 & 1.\times 10^{18} & 0 & 1.\times 10^{27} \\ 1.\times 10^{11} \text{X} & 0 & 0 & 1.\times 10^{27} & 0 \\ \end{array} \right) $$

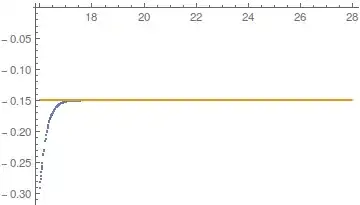
as a function of $X$. The result using Eigenvectors are quite strange and I assume there is some numerical error here. The two eigenvectors with the smallest eigenvalues consist mostly of the second and fourth component $(0,a,0,b,0)$. The following image shows $a$ and $b$ for the eigenvector with the smallest eigenvalue as a function of $X$. Both axes are shown as $Log_{10}$.

Up to $X\approx 10^{19}$ this eigenvector consists of almost equal parts of $a$ and $b$. Then, suddenly it jumps and the eigenvector consists almost exclusively of $b$. The behavior at bigger values of $X$ is even stranger. Any idea what goes wrong here, would help me a lot!

I compute the eigenvectors for different values of $X$ using

 X=1.0*10^RandomReal[{16,28}];

Edit: My complete code is:

scanpoints = 1000;
saved1 = Array[f, scanpoints];
saved2 = Array[f, scanpoints];
n = 1; While[n <= scanpoints,
SM = 1.0*10^2;
Su6 = 1.0*10^16;
IS = 1.0*10^11;
Ex6 = 1.0*10^RandomReal[{16, 28}];
Matrix =  1/(Ex6*IS)*{{0, IS*SM + Su6*SM, Ex6*SM, 0, Ex6*IS}, {IS*SM + Su6*SM,
  0, 0, 0, 0}, {Ex6*SM, 0, IS^2, IS*SM + Su6*SM, IS*SM}, {0, 0, 
 IS*SM + Su6*SM, SM^2, Su6*IS + Su6*SM}, {Ex6*IS, 0, IS*SM, 
 Su6*IS + Su6*SM, SM^2}};
saved1[[n]] = {Log10[Ex6],Log10[Abs[(Eigensystem[Matrix])[[2, 5]][[4]]]]};
saved2[[n]] = {Log10[Ex6],Log10[Abs[(Eigensystem[Matrix])[[2, 5]][[2]]]]}; 
n++]

And the plot is generated using:

 ListPlot[{saved1, saved2}]

What happens if you don't use machine precision?, i.e. x = 10^RandomReal[{16,28}]; — dr.blochwave, Dec 01 '15 at 13:59
You are working with values that have scale differences as large as a factor 10^25 or so. Machine arithmetic precision is not likely to be adequate for that. Also it would be helpful if the entire problem were posed in Mathematica format; I certainly am not going to enter that matrix by hand to do any testing. — Daniel Lichtblau, Dec 01 '15 at 16:13
@DanielLichtblau Thanks for your comment. I added my code to the question. — jak, Dec 01 '15 at 16:34
one thing to consider is your assumption re: the ordering of the eigenvectors may not be correct, see here: http://mathematica.stackexchange.com/q/83906/2079 — george2079, Dec 01 '15 at 19:25

score 3 · Accepted Answer · answered Dec 01 '15 at 17:36

As per prior comment, it does seem to be an issue of inadequate precision for the task at hand. Here I redo but with matrix elements at 50 digits precision.

scanpoints = 1000;
SM = 10^2;
Su6 = 10^16;
IS = 10^11;
Timing[result = Table[
    Ex6 = 10^RandomReal[{16, 28}, WorkingPrecision -> 50];
    mat = 
     1/(Ex6*IS)*{{0, IS*SM + Su6*SM, Ex6*SM, 0, 
        Ex6*IS}, {IS*SM + Su6*SM, 0, 0, 0, 0}, {Ex6*SM, 0, IS^2, 
        IS*SM + Su6*SM, IS*SM}, {0, 0, IS*SM + Su6*SM, SM^2, 
        Su6*IS + Su6*SM}, {Ex6*IS, 0, IS*SM, Su6*IS + Su6*SM, SM^2}};
    {Log10[Ex6], Log10[Abs[(Eigensystem[mat])[[2, 5]][[4]]]], 
     Log10[Abs[(Eigensystem[mat])[[2, 5]][[2]]]]}
    , {n, scanpoints}];]

(* {1.010633, Null} *)

ListPlot[{result[[All, 1 ;; 2]], result[[All, {1, 3}]]}]

If that WorkingPrecision -> 50 is removed then one recovers the unwanted picture.

Strange eigenvector behaviour for matrix with large numerical values

1 Answers1