InterpolationOrder has no effect on ListContourPlot when the data is of the form {x,y,f[x,y]}

Question

This is related to the issue brought up here, if you want to mark it as duplicate feel free to do so, but it is slightly separate.

Take two sets of data, identical except for the form,

dta1 = Table[Exp[-x^2] Sin[y], {y, -π, π, π/3}, {x, -8, 8, 1}];
dta2 = Table[{x, y, Exp[-x^2] Sin[y]}, {x, -8, 8, 1}, {y, -π, π, π/3}]~Flatten~1;

The first is a two-dimensional array and the second is a list of tuples. Now note the different effects of InterpolationOrder on these data,

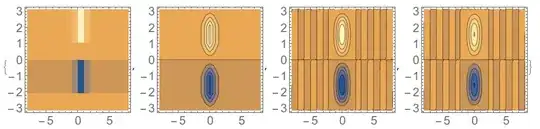
ListContourPlot[dta1, InterpolationOrder -> #, ImageSize -> 200, 
   DataRange -> {{-8, 8}, {-π, π}},PlotRange-> All] & /@ {0, 1, 2, 3}

ListContourPlot[dta2, InterpolationOrder -> #, 
   ImageSize -> 200,PlotRange -> All] & /@ {0, 1, 2, 3}

Going past an order of 1 has no effect. At order zero they are identical, at order 1 the 2D array is already better.

Notice that this is not a problem for ListLinePlot with one-dimensional data

func = Exp[-#^2] Cos[4 #] &;
list1 = Table[func[x], {x, -5, 5, .5}];
list2 = Table[{x, func[x]}, {x, -5, 5, .5}];
ListLinePlot[list1, DataRange -> {-5, 5}, InterpolationOrder -> #, 
   PlotRange -> {-1, 1}, ImageSize -> 200] & /@ {0, 1, 2, 3}
ListLinePlot[list2, InterpolationOrder -> #, PlotRange -> {-1, 1}, 
   ImageSize -> 200] & /@ {0, 1, 2, 3}