How to pick an element of a row corresponding to the minimum in a particular column?

Question

How can I find what value in column 1 of my list corresponds to the minimum value in column 2?

Hi @belisarius, I just saw this. This is my first use of this website, and so far it is very helpful. I did need to know the value, and now I'd also like to find out how to find the position in the array. Thank you! — Michelle, Sep 03 '12 at 03:37

score 15 · Answer 1 · answered Sep 03 '12 at 03:20

15

Pick[] is one way to go about it:

test = {{15, 11}, {5, 14}, {2, 13}, {3, 5}, {13, 15}, {6, 10}, {8, 15}, {0, 2},
        {10, 13}, {2, 5}};

Pick[#1, #2, Min[#2]] & @@ Transpose[test]
   {0}

answered Sep 03 '12 at 03:20

J. M.'s missing motivation

124,525
11
401
574

Thank you very much I used your method and it worked! – Michelle Sep 03 '12 at 03:29
Can I also find which item in the array the minimum value is? How? – Michelle Sep 03 '12 at 03:34
@Michelle did you read my comment right under your question? – Dr. belisarius Sep 03 '12 at 03:35
Hi @belisarius, I just saw it. This is my first visit to the website and I did not at first notice that I needed to "expand" the new comments. – Michelle Sep 03 '12 at 03:37
@Michelle Welcome! It takes some time to get used to the features of the site. Feel free to ask – Dr. belisarius Sep 03 '12 at 03:39
@belisarius thank you! I also need to know the position in the array that corresponds to the minimum value in the 2nd column. I have tried many things and cannot figure it out. I might be making a small mistake, as a Junior in Physics I am not familiar with Mathematica yet. – Michelle Sep 03 '12 at 03:40
@Michelle {Min[#2], Position[#1, Min[#2]]} & @@ Transpose[test] – Dr. belisarius Sep 03 '12 at 03:47
@Michelle, "Can I also find which item in the array the minimum value is?" - Pick[Thread[{#1, #2}], #2, Min[#2]] & @@ Transpose[test] and Pick[#, #[[All, 2]], Min[#[[All, 2]]]] &[test] are two ways to do it. You get a $p\times 2$ array, where $p$ is the number of results returned; for each entry, the second component is the minimum value in the second column, and the first component is the corresponding entry in the first column. – J. M.'s missing motivation Sep 03 '12 at 04:14
I interpreted "corresponds to" as meaning equals! – DavidC Sep 03 '12 at 17:55

DavidC · Answer 2 · 2012-09-05T13:44:47.967

Edit

In my earlier submission, I mistakenly took "corresponds to" as meaning "has the same value as". Here I interpret "corresponds to" as "occupies the same row as". This variation relies on Position, as before.

#1[[Position[#2, Min@#2][[1, 1]]]] & @@ Transpose@t

Exemplification

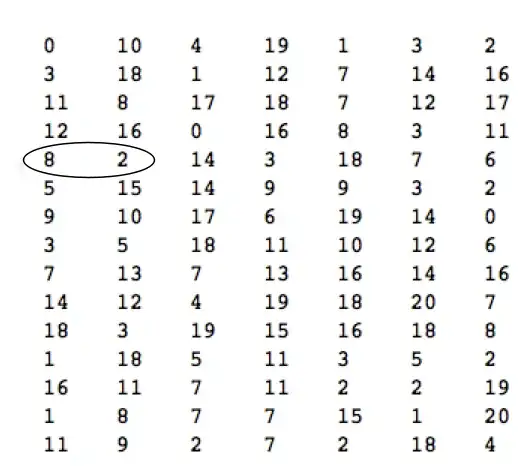
t happens to be 15x7:

t={{0, 10, 4, 19, 1, 3, 2}, {3, 18, 1, 12, 7, 14, 16}, {11, 8, 17, 18, 7, 12, 17}, {12, 16, 0, 16, 8, 3, 11}, {8, 2, 14, 3, 18, 7, 6}, {5, 15, 14, 9, 9, 3, 2}, {9, 10, 17, 6, 19, 14, 0}, {3, 5, 18, 11, 10, 12, 6}, {7, 13, 7, 13, 16, 14, 16}, {14, 12, 4, 19, 18, 20, 7}, {18,3, 19, 15, 16, 18, 8}, {1, 18, 5, 11, 3, 5, 2}, {16, 11, 7, 11, 2, 2, 19}, {1, 8, 7, 7, 15, 1, 20}, {11, 9, 2, 7, 2, 18, 4}}

The lowest value in column 2 is 2. It sits next to the value 8 in column one.

#1[[Position[#2, Min@#2][[1, 1]]]] & @@ Transpose@t

8

results

Explanation

Let's explain what the following does:

#1[[Position[#2, Min@#2][[1, 1]]]]

First note that Min@#2returns the minimum value in the second column: 2

Now plug 2 into

Position[#2, Min@#2][[1, 1]]

obtaining

Position[#2, 2][[1, 1]]

returning `5'.

Substituting again, #1[[5]] returns the value the cell at column 1, row 5:

8

score 4 · Answer 3 · answered Sep 03 '12 at 03:19

4

Here's a straightforward way using Cases:

list = {{1, 2}, {2, 2}, {3, 1}, {4, 1}, {2, 4}}; (* example list *)
With[{min = Min@#[[All, 2]]}, Cases[#, {x_, min} :> x]] &@list
(* {3, 4} *)

You can also use Select or Pick, depending on the usage. You should read through the documentation to see how to use them.

answered Sep 03 '12 at 03:19

rm -rf

88,781
21
293
472

Thank you very much I used Pick[] and it worked. – Michelle Sep 03 '12 at 03:36

Rojo · Answer 4 · 2012-09-03T04:31:48.303

4

Here's another way, stealing @J.M's test list

test = {{15, 11}, {5, 14}, {2, 13}, {3, 5}, {13, 15}, {6, 10}, {8, 15}, {0, 2},
        {10, 13}, {2, 5}};

First@Extract[test, test~Reverse~2~Ordering~1]

0

Remove First to see the whole row

Or probably faster is

Extract[#1, #2~Ordering~1] & @@ Transpose[test]

edited Sep 03 '12 at 04:31

answered Sep 03 '12 at 03:43

Rojo

42,601
7
96
188

Damn, you win the cool factor. – kale Sep 03 '12 at 03:44
Rojo~Reverse~Upvote – Dr. belisarius Sep 03 '12 at 03:49
@belisarius, haha, I almost did it on purpose waiting for your comment – Rojo Sep 03 '12 at 03:50
I knew. I tried hard not to fail you – Dr. belisarius Sep 03 '12 at 03:50

score 2 · Answer 5 · answered Sep 03 '12 at 03:11

Sure.

Not sure about "asking" but here's a way to do it.

I'll build some data for an example:

a = RandomReal[{0, 10}, {10, 2}]

And to find the value in the position in column 1 of the minimum of column 2:

a[[Flatten[Position[a[[All, 2]], Min[a[[All, 2]]]]], 1]]

Romke Bontekoe · Answer 6 · 2012-09-03T08:05:49.380

Beware of the possibility of multiple minima, especially in long lists of discrete elements. I think for a novice J.M.'s solution is the more instructive. I have changed its first element to demonstrate two identical minima:

test = {{15, 2}, {5, 14}, {2, 13}, {3, 5}, {13, 15}, {6, 10}, {8, 15}, {0, 2}, {10, 13}, {2, 5}};

Pick[#1, #2, Min[#2]] & @@ Transpose[test]

out: {15, 0}

Finding the position of the minimum/minima:

min = Min@test[[All, 2]]
pos = Position[test[[All, 2]], min]

out: 2
out: {{1}, {8}}

In order to grab the corresponding values in Col. 1, the "pos" list must be Flattened first:

test[[Flatten@pos, 1]]

out: {15, 0}

kglr · Answer 7 · 2012-09-05T22:35:02.900

2

With

test = {{15, 11}, {5, 14}, {2, 13}, {3, 5}, {13, 15}, {6, 10}, {8, 15},
    {0,2}, {10, 13}, {2, 5}};

variations with Ordering in Rojo's answer using Part instead of Extract:

test[[Ordering[test[[All, 2]], 1]]][[1, 1]]

or

First[#[[1]][[Ordering[#[[2]], 1]]] &[Transpose[test]]]

or

test[[Ordering[test, 1, #1[[2]] < #2[[2]] &]]][[1, 1]]
(* 0 *)

edited Sep 05 '12 at 22:35

answered Sep 05 '12 at 21:59

kglr

394,356
18
477
896

score 1 · Answer 8 · answered Sep 20 '23 at 10:20

Using two newer functions:

test = {{15, 11}, {5, 14}, {2, 13}, {3, 5}, {13, 15}, {6, 10}, {8, 15}, {0, 2}, {10, 13}, {2, 5}};
MinimalBy[test, Last][[1, 1]]

0

First @ Extract[PositionSmallest[Last /@ test]] @ test

0

MinimalBy since V 10.3

PositionSmallest since V 13.2

E. Chan-López · Answer 9 · 2023-09-20T22:26:37.607

Another way, using Query and SelectFirst:

f[mat_] := mat // Query[SelectFirst[#[[2]] == Min[mat[[All, 2]]] &], 1]

Testing f:

test = {{15, 11}, {5, 14}, {2, 13}, {3, 5}, {13, 15}, 
       {6, 10}, {8, 15}, {0, 2},{10, 13}, {2, 5}};
t={{0, 10, 4, 19, 1, 3, 2}, {3, 18, 1, 12, 7, 14, 16}, {11, 8, 17, 18, 7, 12, 17}, 
  {12, 16, 0, 16, 8, 3, 11}, {8, 2, 14, 3, 18, 7, 6}, {5, 15, 14, 9, 9, 3, 2}, 
  {9, 10, 17, 6, 19, 14, 0}, {3, 5, 18, 11, 10, 12, 6}, {7, 13, 7, 13, 16, 14, 16}, 
  {14, 12, 4, 19, 18, 20, 7}, {18,3, 19, 15, 16, 18, 8}, {1, 18, 5, 11, 3, 5, 2}, 
  {16, 11, 7, 11, 2, 2, 19}, {1, 8, 7, 7, 15, 1, 20}, {11, 9, 2, 7, 2, 18, 4}};
f /@ {test, t}
({0, 8})

How to pick an element of a row corresponding to the minimum in a particular column?

9 Answers9

Linked