14

I have a graphics expression which renders nicely as a closed curve when put in Graphics, I don't understand why I can't get the lines from DiscretizeGraphics or BoundaryDiscretizeGraphics:

 p = {BSplineCurve[{{0.1288208346384372`, 
         0.24716061799090383`}, {0.18307091717113483`, 
         0.29633799186027077`}, {0.18104183370580254`, 
         0.25496700929944494`}, {0.22444189973196066`, 
         0.2943089083949385`}, {0.18307091717113483`, 
         0.29633799186027077`}, {0.23732099970383244`, 
         0.34551536572963765`}}, SplineWeights -> {1, 15, 25, 25, 15, 1}],
       BSplineCurve[{{0.1288208346384372`, 
         0.47866942629949966`}, {0.18307091717113483`, 
         0.41209239601456865`}, {0.13474007204408336`, 
         0.417023175115462`}, {0.17814013807024148`, 
         0.3637615508875172`}, {0.18307091717113483`, 
         0.41209239601456865`}, {0.23732099970383244`, 
         0.34551536572963765`}}, SplineWeights -> {1, 15, 25, 25, 15, 1}],
       Line[{{0.1288208346384372`, 
         0.24716061799090383`}, {0.1288208346384372`, 
         0.47866942629949966`}}]}
{Graphics@p, DiscretizeGraphics[p]}

![enter image description here

I looked though the options but couldn't find any PlotPoints like option.

J. M.'s missing motivation
  • 124,525
  • 11
  • 401
  • 574
M.R.
  • 31,425
  • 8
  • 90
  • 281
  • PlotRange doesn't seem to be the issue. However, for reasons that I don't fully understand, removing the SplineWeights in your BSplineCurves improves the situation, but doesn't solve it completely. – MarcoB Dec 09 '15 at 02:17
  • @MarcoB yes is see that, better but still has wholes... weird! – M.R. Dec 09 '15 at 05:09
  • Annoyingly, JoinedCurve[] does not play well with DiscretizeGraphics[]. – J. M.'s missing motivation Dec 09 '15 at 05:13
  • I don't now the exact answer but my guess is the problem is with line and BSplineCurve combination. The line is bounded piece wise linear primitive and BSplineCurve is a nonlinear primitive with an only approximation represented. If you try BoundaryDiscretizeGraphics you get an error saying 'BoundaryMeshRegion::buncl: At least one boundary was not closed in'. So the line and spline joined points does not overlap due to approximation of spline. – s.s.o Dec 09 '15 at 10:28
  • @s.s.o how can I fix that – M.R. Dec 10 '15 at 19:47
  • Hi, you have asked once a question about indenting sub cells like text to last item etc. Can't find it now, could you point me to it? – Kuba Dec 11 '15 at 07:38
  • BezierCurve won't discretize correctly (there's a bug). http://mathematica.stackexchange.com/q/98147/12 I haven't read your question in detail, but I thought I should warn you about this in case BSplineCurve has problems too. – Szabolcs Dec 11 '15 at 08:56

2 Answers2

13

So DiscretizeGraphics seems to always miss the first or last point of a BSplineCurve (it seems to do it with a BezierCurve as well). Here's the simplest example of this,

pts = {{.5, 0}, {1, 0}, {1, 1}, {.5, 1}, {0, 1}, {0, 0}, {.5, 0}};
GraphicsRow[{Graphics@#, DiscretizeGraphics@#} &@BSplineCurve[pts], 
 ImageSize -> 600]

enter image description here

Why does it do this? Not sure, hopefully one of the kernel developers that hang around here can chime in. It seems at first to be related to this problem with discretizing Bezier curves, but there you have the problem that BezierFunction is awful. Here we have a workaround, because BSplineFunction works just fine.

Just extract the points from the curve, create a Line object from them, and discretize that. Inspiration came from this answer over on stackoverflow,

discretizableBSplineCurve[pts_, opts : OptionsPattern[]] := 
 Line@(BSplineFunction[pts, 
     Evaluate[FilterRules[{opts}, Options[BSplineCurve]]]] /@ 
    Range[0, 1, .01])

Trying it on the above case,

GraphicsRow[{Graphics@#, DiscretizeGraphics@#} &@
  discretizableBSplineCurve[pts], ImageSize -> 600]

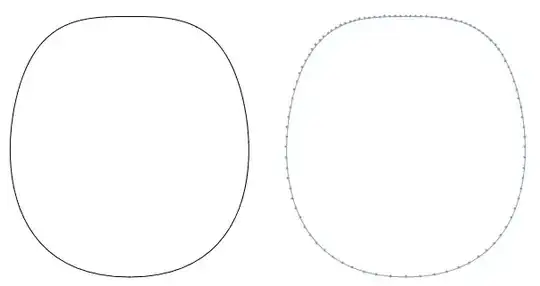
enter image description here

Here it is applied to puzzle piece M.R. is drawing,

p1 = {discretizableBSplineCurve[{{0.1288208346384372`, 
      0.24716061799090383`}, {0.18307091717113483`, 
      0.29633799186027077`}, {0.18104183370580254`, 
      0.25496700929944494`}, {0.22444189973196066`, 
      0.2943089083949385`}, {0.18307091717113483`, 
      0.29633799186027077`}, {0.23732099970383244`, 
      0.34551536572963765`}}, 
    SplineWeights -> {1, 15, 25, 25, 15, 1}], 
   discretizableBSplineCurve[{{0.1288208346384372`, 
      0.47866942629949966`}, {0.18307091717113483`, 
      0.41209239601456865`}, {0.13474007204408336`, 
      0.417023175115462`}, {0.17814013807024148`, 
      0.3637615508875172`}, {0.18307091717113483`, 
      0.41209239601456865`}, {0.23732099970383244`, 
      0.34551536572963765`}}, 
    SplineWeights -> {1, 15, 25, 25, 15, 1}], 
   Line[{{0.1288208346384372`, 
      0.24716061799090383`}, {0.1288208346384372`, 
      0.47866942629949966`}}]};
{Graphics@p1, DiscretizeGraphics[p1]}

enter image description here

Another way to do it would be to modify 'DiscretGraphics, that way you can work with objects that still have the headBSplineCurve`. 

discretizeGraphics2[graphics_] := 
 DiscretizeGraphics@(graphics /. {BSplineCurve[
       a__] :> (Line@(BSplineFunction[a] /@ Range[0, 1, .01]))});

Trying this on p as defined in the OP,

{DiscretizeGraphics@p, discretizeGraphics2@p}

enter image description here

Edit So I'm looking at that last picture and thinking that they don't look identical, and wondering if my strategy of converting to a line first messes up the graphic. But when compared to the original, un-discretized version, my system produces a much more faithful reproduction when pre-converting the curve:

GraphicsRow[{Show[{Graphics@p, DiscretizeGraphics@p}], 
  Show[{Graphics@p, discretizeGraphics2@p}]}]

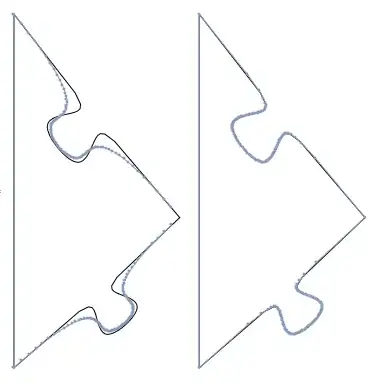
enter image description here

And I can't seem to improve the plot on the left with any combination of options to DiscretizeGraphics (AccuracyGoal, PerformanceGoal, PrecisionGoal, or MeshQualityGoal). It must be possible, as M.R.'s DiscretizeGraphics in his example image looks much better than mine. I'm using version 10.2, perhaps it has been improved in version 10.3?

Edit2 Following J.M.'s suggestion, I've worked up a version that uses ParametricPlot to adaptively sample the BSplineFunction. It seems to be an order of magnitude slower (not that it is all that slow), and ends up plotting many more points, but it could lead to a more faithful reproduction of the original BSplineCurve objects,

discretizeGraphics2b[graphics_] := 
 DiscretizeGraphics@(graphics /. {BSplineCurve[
       a__] :> (Line@(Cases[
          ParametricPlot[BSplineFunction[a][t], {t, 0, 1}], 
          Line[{x__}] :> x, \[Infinity]]))});

{discretizeGraphics2@p,
 discretizeGraphics2b@p}

enter image description here

Community
  • 1
Jason B.
  • 68,381
  • 3
  • 139
  • 286
  • For the first part you can use pts = {{.5, 0}, {1, 0}, {1, 1}, {.5, 1}, {0, 1}, {0, 0}}; Graphics@BSplineCurve[pts, SplineClosed -> True] so that you don,'t need to duplicate the first or last point. There is a bug I thing in DiscretizeGraphics. It forgets to ckeck if the shape is closed. And algorithm skips the last segment. – s.s.o Dec 11 '15 at 09:54
  • ahhh, I don't know much about BSplineCurve, I grabbed that list of points from the help page. But even for a non-closed BSplineCurve, DiscretizeGraphics will omit points. Try this, gr = Graphics[{BezierCurve[{{0, 1}, {1, 1}, {2, -1}, {5, 2}}]}]; dgr = DiscretizeGraphics[gr]; Show[gr, dgr] – Jason B. Dec 11 '15 at 09:57
  • Yes, I think here is a bug in DiscretizeGraphics algorithm skips the last segment. – s.s.o Dec 11 '15 at 10:09
  • You might consider using ParametricPlot[] to adaptively sample your BSplineFunction[]. – J. M.'s missing motivation Dec 11 '15 at 11:22
  • @J.M. then how do I combine the graphics together? If I just use Show[g1,g2] where g1 and g2 are two different ParametricPlots, with different PlotRanges, it won't show the whole thing. But if they are Line objects, Graphics[g1,g2] automatically shows everything. – Jason B. Dec 11 '15 at 11:44
  • Scratch that, if I apply PlotRange->All then I can combine them, but it does require and extra Show, meaning that I need to supply a Graphics to the Line object from p in order to combine them. How would I evaluate whether this was better? – Jason B. Dec 11 '15 at 11:47
  • Well, after using ParametricPlot[], you could extract the Line[] object representing the curve, after a preprocessing with Normal[] to get rid of GraphicsComplex[]. – J. M.'s missing motivation Dec 11 '15 at 11:49
  • It seems to work without Normal, thanks for the tip – Jason B. Dec 11 '15 at 12:12
7

An alternate, i suspect faster, way to get your evenly spaced points, using linepoints from here: https://mathematica.stackexchange.com/a/39457/2079

DiscretizeGraphics@
 Line[linepoints[
    Table[ BSplineFunction[{{0.1288208346384372`, 
         0.24716061799090383`}, {0.18307091717113483`, 
         0.29633799186027077`}, {0.18104183370580254`, 
         0.25496700929944494`}, {0.22444189973196066`, 
         0.2943089083949385`}, {0.18307091717113483`, 
         0.29633799186027077`}, {0.23732099970383244`, 
         0.34551536572963765`}}, 
       SplineWeights -> {1, 15, 25, 25, 15, 1}][t] , {t, 0, 
      1, .001}] , 50]~Join~
   linepoints[
    Table[BSplineFunction[{{0.1288208346384372`, 
         0.47866942629949966`}, {0.18307091717113483`, 
         0.41209239601456865`}, {0.13474007204408336`, 
         0.417023175115462`}, {0.17814013807024148`, 
         0.3637615508875172`}, {0.18307091717113483`, 
         0.41209239601456865`}, {0.23732099970383244`, 
         0.34551536572963765`}}, 
       SplineWeights -> {1, 15, 25, 25, 15, 1}][t] , {t, 1, 
      0, -.001}], 50]~
   Join~{{0.1288208346384372`, 
     0.24716061799090383`}, {0.1288208346384372`, 
     0.47866942629949966`}}]

enter image description here enter image description here

(second version obtained applying linepoints to the straight edge line as well )

Community
  • 1
george2079
  • 38,913
  • 1
  • 43
  • 110