How to demodulate an FM signal in continuous-time?

Question

I'm not sure if this is a math or Mathematica question, but I'm posting it here because I'm interested in possible Mathematica tools/functions to solve the problem.

I'm stuck. I want to simulate the effect of a EMP (ElectroMagnetic Pulse) disturbance on an FM signal. Here's my code:

f1[t_] := Sin[t]; (* baseband signal *)
f2[t_] := Sin[15 t]; (* carrier *)
f3[t_] := Sin[15 t + 8 f1[t]] ; (* antenna signal *)
f4[t_] := UnitTriangle[2 (t - 4)]; (* lightning EMP *)
f5[t_] := f3[t] + f4[t]; (* received signal *)
Plot[{f5[t], f1[t]}, {t, 0, 20}]

which results in this plot:

So far so good, but here I am stuck. I want to demodulate the received signal to see the effect of the EMP on my baseband signal, and I don't know how to do this. The signal is there, I can see it (and hear it when I listen to the radio).

I prefer a continuous-time solution, because that's what my radio also works in, but if necessary a discrete-time solution is also welcome.

Answer 1

Here is my port of fmmod/fmdemod from MATLAB to Mathematica.

First off, I know very very little about signal processing, but I have verified that this function gives the same answers as the MATLAB function.

1. fmmod: uses the message signal x to modulate the carrier frequency fc (Hz) and sample frequency fs (Hz), where fs > 2*fc. freqdev (Hz) is the frequency deviation of the modulated signal.

   fmmod[x_, fc_, fs_, freqdev_] := Module[{t1, intx}, If[fs < 2*fc, Return[$Failed]];
   t1 = Range[0, ConstantArray[#2 - 1, #1] & @@ Dimensions[x]/fs, 1/fs];
   intx = Accumulate[x]/fs;
   Cos[2*Pi*fc*t1 + 2*Pi*freqdev*intx] // Transpose];
   

2. fmdemod: demodulates the FM modulated signal y at the carrier frequency fc (Hz). y and fc have sample frequency fs (Hz). freqdev is the frequency deviation (Hz) of the modulated signal. I'm still fighting with this algorithm. Mainly the unwrap function. Maybe someone can help.

Hope this helps somewhat.

EDIT: Okay, I've had a little more time to stew on this. Sadly, I can't get a working continuous function with MATLAB's method (using the Hilbert transform). Here is a discrete fmdemod procedure that returns a demodulated signal. This uses J. M.'s discrete Hilbert transform found here. I also found an Unwrap function here.

For your example, let's define a couple necessary functions first.

hilbert[data_?VectorQ] := Block[{n, e},
   e = Boole[EvenQ[n = Length[data]]];
   InverseFourier[PadRight[
      ArrayPad[ConstantArray[2, Quotient[n, 2] - e], {1, e}, 1], 
      n] Fourier[data, FourierParameters -> {1, -1}], 
    FourierParameters -> {1, -1}]] /; And @@ Thread[Im[data] == 0]

UnwrapPhase[data_?VectorQ, tol_: Pi, inc_: 2 Pi] := 
 FixedPoint[# + 
    inc*FoldList[Plus, 0., 
      Sign[Chop[ListCorrelate[{1, -1}, #], tol] ] ] &, data]

UnwrapPhase[list : {{_, _} ..}] := 
 Transpose[{list[[All, 1]], UnwrapPhase[list[[All, -1]]]}]

Now to the main function:

fmdemod[y_, fc_, fs_, freqdev_, iniphase_] := Module[{t1, yq},
   t1 = Range[0, (Length[y] - 1)/fs, 1/fs];
   yq = hilbert[y]*Exp[-I*2 Pi*fc*t1 - iniphase];
   (Prepend[Differences[UnwrapPhase[Arg[yq]]], 0]*fs)/(2 Pi*freqdev)];

So using:

f1[t_] := Sin[t]; (* baseband signal *)
f2[t_] := Sin[15 t]; (* carrier *)
f3[t_] := Sin[15 t + 8 f1[t]] ; (* antenna signal *)
f4[t_] := UnitTriangle[2 (t - 4)]; (* lightning EMP *)
f5[t_] := f3[t] + f4[t]; (* received signal *)
Plot[{f5[t], f1[t]}, {t, 0, 20}]

Therefore:

fc = 15; (*carrier frequency*)
fm = 8; (*modulated frequency*)
fs = 100; (*sampling rate*)
t = Range[0., 20, 2 Pi/fs];
y = Sin[fc* t + fm* Sin[t]] + UnitTriangle[2 (t - 4)];
z = fmdemod[y, fc, fs, 1, 0];
ListPlot[{Transpose[{t, z}], Transpose[{t, fm*Sin[t + Pi/2]}]}, 
 Joined -> True]

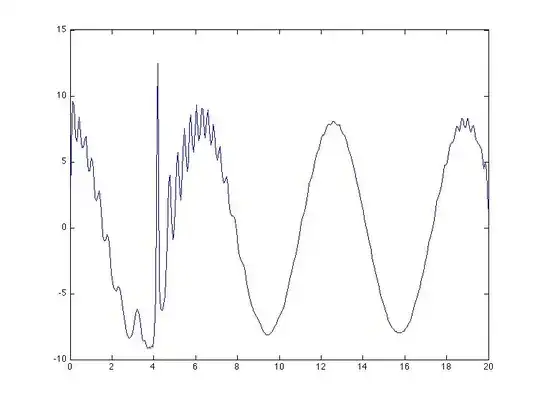
Which outputs a demodulated signal with lightning static.

BTW, verified in MATLAB as z = fmdemod(y,15,100,1):