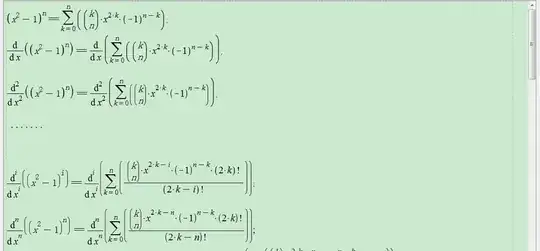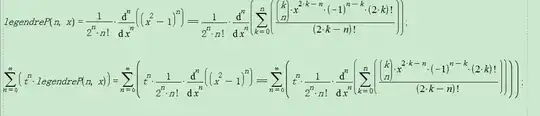-5

[![enter image description here][1]][1]

I was wondering how to get the following result by mathematica or maple or other way

I have asked this question several days ago and recently I have got some new ideas,in the last equation of my new submitted pictures ,WE can got the simplest result of the left formula is!(1/\@(1 + t\^2 - 2\ t\ x)),so the right formula is also this result ,but in mathematica I get the result of thr right formula a Hypergeometric Function,so I was wondering how to get the simplest result as the left formula?

enter image description hereenter image description here

dcydhb
  • 615
  • 3
  • 9

1 Answers1

6

One would hope that 

Sum[t^n D[(x^2 - 1)^n, {x, n}] 2^-n/n!, {n, 0, Infinity}]

would yield the desired result, but it returns unevaluated. However, according to Wolfram Mathworld,

LegendreP[n, x] == D[(x^2 - 1)^n, {x, n}] 2^-n/n!

for n a nonnegative integer. Using this identity to rewrite the Sum then gives

Sum[LegendreP[n, x] t^n, {n, 0, Infinity}]
(* 1/Sqrt[1 + t^2 - 2 t x] *)

as desired.

As Simon Woods noted in a comment below, Mathematica apparently cannot handle symbolic multiple derivatives. With a specific value of n, for instance

With[{n = 30}, FullSimplify[LegendreP[n, x] == D[(x^2 - 1)^n, {x, n}] (1/2)^n/n!]]
(* True *)

Mathematica recognizes the identity.)

Community
  • 1
bbgodfrey
  • 61,439
  • 17
  • 89
  • 156