Part 1 - Eliminate p
I am not sure this is what you are looking for but both Solve and Reduce give solutions.
When I evaluate q1 and q2 I get
pp[n_Integer] := If[n > 0, pp[n - 1]^2 + c, p]
q1 = PolynomialQuotient[pp[4] - p, pp[2] - p, p]
(* 1 + 2 c^2 + 3 c^3 + 3 c^4 +
3 c^5 + c^6 + (2 c + c^2 + 2 c^3 + c^4) p + (c + 5 c^2 + 6 c^3 +
12 c^4 + 6 c^5) p^2 + (1 + 4 c^2 + 4 c^3) p^3 + (4 c + 3 c^2 +
18 c^3 + 15 c^4) p^4 + (2 c + 6 c^2) p^5 + (1 + 12 c^2 +
20 c^3) p^6 + 4 c p^7 + (3 c + 15 c^2) p^8 + p^9 + 6 c p^10 + p^12 *)
q2 = PolynomialRemainder[D[pp[4], p] - 1, q1, p]
(* 15 + 32 c^2 + 48 c^3 + 48 c^4 + 48 c^5 +
16 c^6 + (16 c + 16 c^2 + 16 c^3) p + (16 c + 48 c^2 + 80 c^3 +
160 c^4 + 80 c^5) p^2 +
32 c^2 p^3 + (16 c + 32 c^2 + 192 c^3 + 160 c^4) p^4 +
16 c p^5 + (96 c^2 + 160 c^3) p^6 + (16 c + 80 c^2) p^8 + 16 c p^10 *)
Now apply Solve
solution =
Solve[{1 + 2 c^2 + 3 c^3 + 3 c^4 + 3 c^5 +
c^6 + (2 c + c^2 + 2 c^3 + c^4) p + (c + 5 c^2 + 6 c^3 +
12 c^4 + 6 c^5) p^2 + (1 + 4 c^2 + 4 c^3) p^3 + (4 c +
3 c^2 + 18 c^3 + 15 c^4) p^4 + (2 c + 6 c^2) p^5 + (1 +
12 c^2 + 20 c^3) p^6 + 4 c p^7 + (3 c + 15 c^2) p^8 + p^9 +
6 c p^10 + p^12 == 0,
15 + 32 c^2 + 48 c^3 + 48 c^4 + 48 c^5 +
16 c^6 + (16 c + 16 c^2 + 16 c^3) p + (16 c + 48 c^2 + 80 c^3 +
160 c^4 + 80 c^5) p^2 +
32 c^2 p^3 + (16 c + 32 c^2 + 192 c^3 + 160 c^4) p^4 +
16 c p^5 + (96 c^2 + 160 c^3) p^6 + (16 c + 80 c^2) p^8 +
16 c p^10 == 0}, {c, p}, Complexes];
There is a long list of solutions (some of which have Root) but I won't use up the space showing them. Here is the first:
solution[[1]]
(* {c -> 1/4 - I/2, p -> -(I/2)} *)
Part 2 - Introduce variable t
q2 is changed to include a variable t in place of the 1.
q2 = PolynomialRemainder[D[pp[4], p] - t, q1, p]
(* 16 + 32 c^2 + 48 c^3 + 48 c^4 + 48 c^5 +
16 c^6 + (16 c + 16 c^2 + 16 c^3) p + (16 c + 48 c^2 + 80 c^3 +
160 c^4 + 80 c^5) p^2 +
32 c^2 p^3 + (16 c + 32 c^2 + 192 c^3 + 160 c^4) p^4 +
16 c p^5 + (96 c^2 + 160 c^3) p^6 + (16 c + 80 c^2) p^8 + 16 c p^10 -
t *)
The expression handed to Solve is modified accordingly
solT = Solve[{1 + 2 c^2 + 3 c^3 + 3 c^4 + 3 c^5 +
c^6 + (2 c + c^2 + 2 c^3 + c^4) p + (c + 5 c^2 + 6 c^3 +
12 c^4 + 6 c^5) p^2 + (1 + 4 c^2 + 4 c^3) p^3 + (4 c +
3 c^2 + 18 c^3 + 15 c^4) p^4 + (2 c + 6 c^2) p^5 + (1 +
12 c^2 + 20 c^3) p^6 + 4 c p^7 + (3 c + 15 c^2) p^8 + p^9 +
6 c p^10 + p^12 == 0,
16 + 32 c^2 + 48 c^3 + 48 c^4 + 48 c^5 +
16 c^6 + (16 c + 16 c^2 + 16 c^3) p + (16 c + 48 c^2 + 80 c^3 +
160 c^4 + 80 c^5) p^2 +
32 c^2 p^3 + (16 c + 32 c^2 + 192 c^3 + 160 c^4) p^4 +
16 c p^5 + (96 c^2 + 160 c^3) p^6 + (16 c + 80 c^2) p^8 +
16 c p^10 == t}, {c, p}, Complexes];
Again there are many solutions.
I don't believe there is any hope to create a functionc[t] for that can be used as an input to Plot.
The first solution was used to form a table of values that could be input to ListPlot.
First a table of complex numbers whose absolute value is unity is formed.
tList = Table[k + I Sqrt[1 - k^2], {k, -1, 1, 0.1}]
(* {-1. + 0. I, -0.9 + 0.43589 I, -0.8 + 0.6 I, -0.7 +
0.714143 I, -0.6 + 0.8 I, -0.5 + 0.866025 I, -0.4 +
0.916515 I, -0.3 + 0.953939 I, -0.2 + 0.979796 I, -0.1 + 0.994987 I,
0. + 1. I, 0.1 + 0.994987 I, 0.2 + 0.979796 I, 0.3 + 0.953939 I,
0.4 + 0.916515 I, 0.5 + 0.866025 I, 0.6 + 0.8 I, 0.7 + 0.714143 I,
0.8 + 0.6 I, 0.9 + 0.43589 I, 1. + 0. I} *)
This is used as the input t to get a table of c[t].
solT1 = Table[{t, N[solT[[1, 1, 2]], 30]}, {t, tList}]
(* {{-1. + 0. I, -1.93971 + 0. I}, {-0.9 +
0.43589 I, -1.94168 + 0.000929621 I}, {-0.8 + 0.6 I, -1.94071 -
0.0000163376 I}, {-0.7 + 0.714143 I, -1.94177 +
0.000473936 I}, {-0.6 + 0.8 I, -1.94109 + 0.000180776 I}, {-0.5 +
0.866025 I, -1.94149 + 0.00108421 I}, {-0.4 +
0.916515 I, -1.93945 - 0.000428769 I}, {-0.3 +
0.953939 I, -1.93898 - 0.000332329 I}, {-0.2 +
0.979796 I, -1.93938 + 0.000494942 I}, {-0.1 +
0.994987 I, -1.94207 - 0.000668456 I}, {0. + 1. I, -1.93976 +
0.000452186 I}, {0.1 + 0.994987 I, -1.94271 -
0.00109377 I}, {0.2 + 0.979796 I, -1.9416 + 0.00229018 I}, {0.3 +
0.953939 I, -1.93757 + 0.00229704 I}, {0.4 +
0.916515 I, -1.94232 + 0.00142531 I}, {0.5 +
0.866025 I, -1.93943 + 0.00165118 I}, {0.6 + 0.8 I, -1.94212 -
0.00232099 I}, {0.7 + 0.714143 I, -1.9319 + 0.000202267 I}, {0.8 +
0.6 I, -1.92091 + 0.00870952 I}, {0.9 + 0.43589 I, -1.93432 +
0.00732884 I}, {1. + 0. I, -1.92309 + 0. I}} *)
I don't know how your want to plot the two complex numbers (t vs c[t]).
I chose to plot the real part of t on the x - axis and make two plots with the imaginary part of c[t] on the y -axis.
ListLinePlot[Transpose[{Re[solT1[[All, 1]]], Im[cList[[All, 2]]]}]]
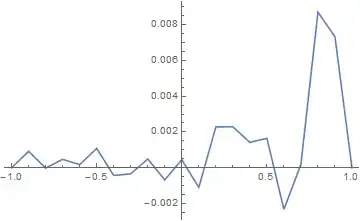
ListLinePlot[Transpose[{Re[solT1[[All, 1]]], Re[solT1[[All, 2]]]}]]
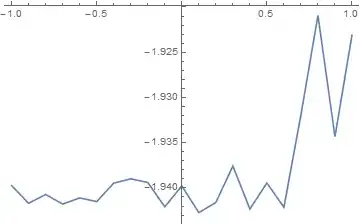


(* Out[315]= {4096 + 12288 c^5 + 4096 c^6 - 768 t + 48 t^2 - t^3 + c^3 (12288 + 256 t) + c^4 (12288 + 256 t) + c^2 (8192 - 256 t - 16 t^2)} *)`
– Daniel Lichtblau Dec 28 '15 at 22:32