5

The equations of the system are

r1 = Sqrt[(x + μ)^2 + y^2 + z^2];
r2 = Sqrt[(x - 1 + μ)^2 + y^2 + z^2];
Ω = (1 - μ)/r1 + μ/r2 + 1/2*(x^2 + y^2) + (μ*(1 - μ))/2;
Ωxz = Ω /. {y -> 0};

μ = 0.0121506683;
xL1 = 0.836914718893202;
xL2 = 1.155682483478613;

And the contour plot of the implicit function is

C0 = 3.201;
P1 = ContourPlot[2*Ωxz == C0, {x, xL1, xL2}, {z, 0, 0.2}, 
ContourShading -> False, ContourStyle -> {Black, Thick}, 
PlotPoints -> 50, PerformanceGoal -> "Speed"]

enter image description here

My question is how to find which value of $x$ corresponds to the maximum value of $z$ and what is the maximum value of $z$.

Similarly the minimum value of $z$ when $C0 = 3.012$.

enter image description here

My question is similar to this however the answers of this questions seem not working in my case.

Community
  • 1
Vaggelis_Z
  • 8,740
  • 6
  • 34
  • 79

2 Answers2

11

You can find the stationary points of $z=z(x)$ by application of the implicit function theorem (to find the derivative of $z$) and solving (numerically) a system of two equations:

stationarypts = 
  {x, z} /. 
    NSolve[{2 Ωxz - C0 == 0, -D[2 Ωxz - C0,x]/D[2 Ωxz - C0, z] == 0}, {x, z}]

 {{-1.0898108637505286, 0. + 0.4183859620455661*I}, 
 {-1.0898108637505286, 0. - 0.4183859620455661*I}, 
 {1.1719884857449565, 0. + 0.07308908417888743*I}, 
 {1.1719884857449565, 0. - 0.07308908417888743*I}, 
 {0.9892920541322313, -0.0984137896912804}, {-0.01369302911651984, 
  0.6235986400369145}, {-0.01369302911651984, -0.6235986400369145}, 
 {0.9892920541322313, 0.0984137896912804}, {0.8365517541212919, 
  0. + 0.011277418446297614*I}, {0.8365517541212919, 0. - 0.011277418446297614*I}}

For the range of values of $x$ you are interest in, there are two stationary points:

Cases[stationarypts, x_ /; xL1 <= x[[1]] <= xL2]

{{0.989292, -0.0984138}, {0.989292, 0.0984138}}

ContourPlot[2 Ωxz - C0 == 0, {x, xL1, xL2}, {z, -0.2, 0.2}, 
  Epilog -> 
    {PointSize[Large], Point[Cases[stationarypts, x_ /; xL1 <= x[[1]] <= xL2]]}]

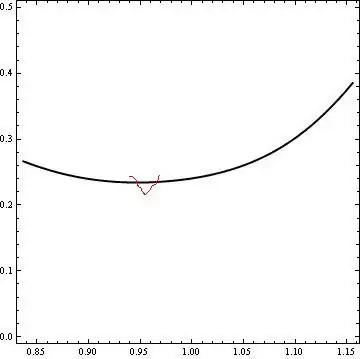
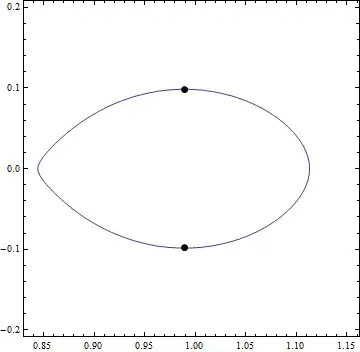
enter image description here

Stelios
  • 1,381
  • 1
  • 11
  • 16
  • 1
    Great work! For C0 = 3.012 the program complains about the complex numbers but this is not important. Many thanks and Merry Christmas! – Vaggelis_Z Dec 25 '15 at 13:39
6
C0 = 3.201;
FindMaximum[{z, 2*Ωxz == C0}, {{x, 1}, {z, 0.1}}]
(*  {0.0984138, {x -> 0.989292, z -> 0.0984138}}  *)

C0 = 3.012;
FindMinimum[{z, 2*Ωxz == C0}, {{x, 1}, {z, 0.1}}]
(*  {0.234294, {x -> 0.947234, z -> 0.234294}}  *)

To get the solution in Finding maximum or minimum of implicit functions to work, bound the variables away from the singularity (vertical tangent) at z == 0:

C0 = 3.201;
Maximize[{z, 2*Ωxz == C0 && xL1 <= x <= xL2 && 0.01 <= z <= 0.2}, {x, z}]
(*  {0.0984138, {x -> 0.989293, z -> 0.0984138}}  *)

C0 = 3.012;
Minimize[{z, 2*Ωxz == C0 && xL1 <= x <= xL2 && 0.01 <= z <= 0.5}, {x, z}]
(*  {0.234293, {x -> 0.947233, z -> 0.234293}}  *)
Community
  • 1
Michael E2
  • 235,386
  • 17
  • 334
  • 747
  • Nice! I played around with FindMaximum but according to documentation the syntax should be FindMaximum[2*Ωxz == C0, {{x, 1}, {z, 0.1}}] which however is not working. What am I missing here? – Vaggelis_Z Dec 25 '15 at 17:45
  • @Vaggelis_Z Doesn't the code in my answer show you what's missing? (I.e., {z, 2*Ωxz == C0} instead of 2*Ωxz == C0, which can't be maximized because it's an equation, not a function.) Note all the syntax forms in the docs. – Michael E2 Dec 25 '15 at 18:00