How to check if a 3D point is in a planar polygon?

Question

Following up on ndroock1's question, I naively tried to apply the solutions to a 3D point and polygon and they didn't work. For example, functions involving ArcTan that are used in kguler's answer don't work with three arguments, Mac's answer doesn't consider the 3rd dimension at all, the undocumented function Graphics`Mesh`PointWindingNumber doesn't work in 3D, and complex numbers only map to 2D planes. And so on.

So, is there any way to check if a 3D point is in a 3D planar polygon?

Answer 1

Just work in local coordinates for the polygon's plane. This requires finding a change of basis matrix and then applying it (which is just matrix multiplication).

One way to obtain a basis is to use any three points on the polygon, assuming they are not collinear. Thus:

basis[{x_, y_, z_, ___}] := Orthogonalize[{y - x, z - x}] // Transpose;

(Orthogonalize is not really necessary but it assures the transformation preserves distances and angles for applications that might need that.)

Right-multiplication by basis[...] converts 3D coordinates to 2D coordinates (ignoring any component of the 3D coordinate orthogonal to the polygon's plane). Then apply whatever 2D algorithm you prefer.

Example

Let's generate a random 3D polygon and another random point:

{vertices, p} = Through[{Most, Last}[RandomReal[NormalDistribution[0, 1], {4, 3}]]];

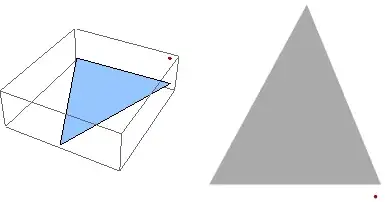
To illustrate the use of basis, here are the 3D and local 2D renderings of this configuration:

Graphics3D[{Polygon[vertices], PointSize[0.02], Darker[Red], Point[p]}]
With[{a = basis[vertices]},
  Graphics[{Lighter[Gray], Polygon[ vertices . a], Darker[Red], PointSize[0.02],  Point[p . a]}]]

---

One check that the point actually is in the plane of the polygon is achieved this way:

inPlane[p_, basis_, origin_] := Abs[Det[Append[Transpose[basis], p - origin]] ] < 10.^(-12)

The origin must be a point known to be in the plane (such as one of the polygon's vertices). E.g.,

inPlane[#, basis[vertices], First[vertices]] &  /@ Append[vertices, p]

{True, True, True, False}

verifies that the triangle does lie in its plane and, as it happens, this particular point does not.

Answer 2

In Version 10, we can use RegionMember to select points that are within a region; whether we're dealing with points in a 3D polygon or a 2D polygon embedded in 3D. Let's take a look at the latter case which is what the OP asks:

We create a triangle embedded in 3D, discretize it and collect points we know for sure are in the triangle:

tri = Triangle[{{0, 0, 0}, {1, 0, 0}, {0, 1, 1}}];
dt = DiscretizeRegion[tri, MaxCellMeasure -> 0.000001];
intri = MeshCoordinates[dt]; (* points in triangle *)

Now we generate random points and mix them with the points created above:

pts = Join[RandomReal[1, {5000, 3}], intri];

We create a RegionMemberFunction and apply it to all points to determine which points are inside/outside the polygon:

rm = RegionMember[dt]

Notice how this tells us we're dealing with a 2D region embedded in 3D. We apply it to all points:

inout = rm[pts];
colors = inout /. {True -> Red, False -> Blue};

Visualize:

Graphics3D[{Transpose[{colors, Point /@ pts}], EdgeForm[Black], Opacity[0], tri}]

Answer 3

I use the algorithm described here for convex 3D polygons. Basically, if a point is inside a polygon, the sum of the angles between the point and each pair of vertices should be $2\pi$, otherwise it's outside the polygon. The angle between two vectors is given by $$\theta=\arccos\left[{\vec a\cdot\vec b\over \|\vec a\|\|\vec b\|}\right].$$ So,

inPolyQ[poly_,pt_]:=2.π==Total[ArcCos[
  Dot@@@#/Times@@@Map[Norm,#,{2}]&@Transpose@{#,RotateRight[#]}
 ]]&@(#-pt&/@poly)

This only works for a convex polygon, however. Additionally, this doesn't check if the polygon is, in fact, planar.

Edit As per J.M.'s comment, this can be simplified using the VectorAngle function:

inPolyQ[poly_,pt_]:=2.π==Total[
  VectorAngle@@@Transpose@{#,RotateRight[#]}
 ]&@(#-pt&/@poly)