Discritizing an analytical 3D-function

Question

I have the following Problem:

I need a discretized amount of points in a 3D-volume. These points satisfy a condition to built-up a 3D-geometry.

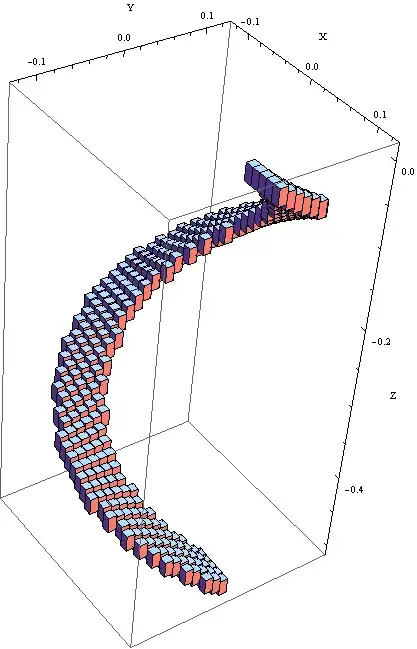
In my example below I selected a helical geometry. The way I found a solution doing the above mentioned is: 1. analytically defining the 3D-volume and Helix function - 2. discretizing

I was wondering if the problem might be easier solved (especially I expierence problems defining the exact functions and limiters for even more complex geometries). I guess discretizing the volume first and checking which Point lie in the desired volume might be easier. However, I do not have a clue, how to do so. Any hints?

I appreciate even simpler ideas!!

(* --- Helix parameters --- *)
HelixRadius = 0.1;
HelixPitch = 0.5;
WireWidth = 0.05;
WireThick = 0.02;

(* --- Defining Volume of interest --- *)
xMin = -0.5;
xMax = 0.5;
Δx = ResXY;
yMin = -0.5;
yMax = 0.5;
Δy = ResXY;
zMin = -0.5;
zMax = 0.5;
Δz = WireThick;

(* --- Resolution for discretization --- *)
ResXY = 0.01;

(* --- Limiters to build-up Helix --- *)
m = HelixPitch/(2 π);
rMin = HelixRadius - WireWidth/2; 
rMax = HelixRadius + WireWidth/2;
kMin = 0; (* switches # of helix turnes integerwise *)
kMax = 0; (* switches # of helix turnes integerwise *)

(* --- Functions defining Helix geometry --- *)
RadiusFunction = Sqrt[x^2 + y^2];
Zfunction = 
  Piecewise[{{m (ArcTan[x/y] + π/2 + k 2 π) - HelixPitch/2, 
     y < 0}, {m (ArcTan[x/y] + 3 π/2 + k 2 π) - HelixPitch/2, 
     y > 0}}, k 2 π];

(* --- Locating Functions to Upper and Lower Limiters --- *)
condition = 
  rMin <= RadiusFunction <= rMax && zMin <= Zfunction <= zMax;

(* --- In table form: coordinates satisfying the above condition and \
wrapping a cuboid around --- *)
tab = Table[
   If[condition , 
    Cuboid[{x, y, 
       Zfunction} - {Δx/2, Δy/
        2, Δz/2}, {x, y, 
       Zfunction} + {Δx/2, Δy/
        2, Δz/2}], {}], {x, xMin, 
    xMax, Δx}, {y, yMin, yMax, Δy}, {k, 
    kMin, kMax}];

(* --- Ploting result in 3D --- *)
PlotCuboids = 
 Graphics3D[tab, Axes -> True, AxesLabel -> {"X", "Y", "Z"}]

Answer 1

What we have to do is select points from a mesh using an analytical function. I can think of two ways. First select the points of its 2D projection and then implement the relation with the third dimension and second, select the points from a 3D mesh.

1. Selecting points within a region using Winding Number

Here I am going to use the undocumented Graphics`PolygonUtils`PointWindingNumber adopted from R.M.'s answer of How to check if a 2D point is in a polygon?

poly[n_, R_] := Table[R {Sin[2 \[Pi] j/n], Cos[2 \[Pi] j/n]}, {j, n}]
inPolyQ[poly_, pt_] := Graphics`Mesh`PointWindingNumber[poly, pt] =!= 0
(*poly creates a polygon and inPolyQ checks if a point (pt) is inside a polygon (poly)*)
L = 10;(*first create a big mesh*)
R1 = 4; R2 = 8;
pts = Flatten[Table[{i, j}, {i, -L, L}, {j, -L, L}], 1];
ring1 = poly[30, R1];  (*regions to select*)
ring2 = poly[30, R2];  (*polygon of order 30 is almost a circle*)
pts1 = Select[pts, inPolyQ[ring2, #] == True && inPolyQ[ring1, #] == False &];
(*from a big mesh (pts) it select all the point within the rings (pts1)*)

pts2 = pts1 /. {x_, y_} -> {x, y, ArcTan[x, y]};
(*convert the 2D data into helix*)
side = {1, 1, 1};
Graphics3D[Cuboid[#, # + side] & /@ pts2]

One advantage here is that you can use any type of mesh (rectangular triangular) to create your initial mesh and then pick out points within any geometry if you can define its vertices.

From V10 you have to use RegionMember which takes the same argument as inPolyQ.

2. Layer wise construction

Here is a way to exactly set given set of conditions. For example a wide helix is defined by two constraints

$R_1^2<x^2+y^2<R_2^2$ and $z = w~Tan^{-1}(y/x)$

So the idea is first you create a mesh on a layer and then select the points with these conditions.

L = 10;(*first create a big mesh*)
R1 = 4; R2 = 8;
w = 0.2;
f1[{x_, y_, z_}] := R1^2 < x^2 + y^2 < R2^2
f2[{x_, y_, z_}] := Abs[Mod[ArcTan[x, y], 2 Pi] - Mod[w z, 2 Pi]] < 0.12
 (*0.12 is the error margin*)
layer[z_] = Flatten[Table[{i, j, z}, {i, -L, L}, {j, -L, L}], 1];(*full layer*)
layerz[z_] := Select[layer[z], f1[#] && f2[#] &] (*selected region*)

nlayer = 80;
Graphics3D[Table[Cuboid[#] & /@ layerz[z], {z, 0, nlayer}],BoxRatios -> {1,1,2}]

I think this one is rather close to what you are looking for.

3. Using parametric equation

You can use your analytic conditions to construct parametric form of coordinates (caution: it may need more work from you than mathematica). Then the job becomes much simpler. For example the parametric form of helix is {r Cos[z], r Sin[z], w z}.

r1 = 3; r2 = 4; dr = 0.25;
w=1;
z1 = 0; z2 = 4 Pi; dz = Pi/30;
pts = Flatten[Table[{r Cos[z], r Sin[z], w z}, 
        {z, z1, z2, dz}, {r, r1, r2, dr}], 1];
side = {dr, dr, 3dz};
Graphics3D[Cuboid[#, # + side] & /@ pts]

Answer 2

Not really clear what you are asking but you might find the region tools useful:

I could not unravel your code to readily get this to work for the helix but here is a simple example of a spherical region.

s = ImplicitRegion[ 
  Norm[ {x, y, z} ] < 1 , { {x, -2, 2}, {y, -2, 2}, {z, -2, 2}}]

points on a grid in the region:

Graphics3D@
 Point@Select[ 
   Flatten[Table[ {x, y, z}, {x, -2, 2, .1}, {y, -2, 2, .1}, {z, -2, 
      2, .1}], 2],
   RegionMember[ s, # ] &] 

with Cuboid instead of Point

random points:

Graphics3D@
 Point[{x, y, z} /. # & /@ 
   FindInstance[ RegionMember[ s , {x, y, z}] , {x, y, z}, 2000]]