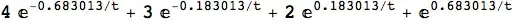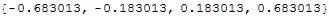3

I have a list 

list00 =
{ E^(-0.6830132/t), E^(-0.6830131/t), E^(-0.6830134/t), E^(-0.68301335/t),  
  E^(-0.18301321/t),E^(-0.18301341/t), E^(-0.1830133/t) , E^(0.183013/t), 
  E^(0.1830132/t) ,E^(0.6830132/t)};

Actually I want to have a summation result as:4E^(-0.683013/t)+3E^(-0.183013/t)+2E^(0.183013/t)+E^(0.683013/t)

In fact the numbers are in another list

list =
 {-0.6830132, -0.6830131, -0.6830134,-0.68301335,  
 -0.18301321, -0.18301341, -0.1830133 , 0.183013, 0.1830132 ,0.6830132};

I have used of Sum[E^(list[[k]]/t),{k,Length[list]})]

eldo
  • 67,911
  • 5
  • 60
  • 168
Unbelievable
  • 4,847
  • 1
  • 20
  • 46

3 Answers3

3
list = {-0.6830132, -0.6830131, -0.6830134, -0.68301335, -0.18301321, \
-0.18301341, -0.1830133, 0.183013, 0.1830132, 0.6830132};

To use of Mean of the values in each cluster

Tr[Length[#]*E^(Mean[#]/t) & /@ GatherBy[list, Round[#, 10^-6] &]]

enter image description here

Bob Hanlon
  • 157,611
  • 7
  • 77
  • 198
2
uni = Union[list, SameTest -> (Abs[#1 - #2] < 10^-4 &)]

enter image description here

Total[Range[Length@uni, 1, -1] E^(uni/t)]

enter image description here

eldo
  • 67,911
  • 5
  • 60
  • 168
  • besides thanks for answer but I cannot use of Union in general. Union lessens my elements. It is true for this case only, because my coefficients are 4...3...2...1 but for a general case I cannot use of Union!!! – Unbelievable Jan 08 '16 at 14:06
2

You can just round the result, and then they are the same number. 

Total[E^(Round[list, 10.^-6]/t)]
(* 4 E^(-0.683013/t) + 3 E^(-0.183013/t) + 
 2 E^(0.183013/t) + E^(0.683013/t) *)

The Exp and Round function are listable, so you don't need an explicit call to Sum. But if you wanted one, 

Sum[ E^(Round[list[[k]], 10.^-6]/t), {k, Length[list]}]

Edit You can also use SetPrecision

Total@Exp[ SetPrecision[list, 6]/t] 

(* 4 E^(-0.683013/t) + 3 E^(-0.183013/t) + 
 2 E^(0.183013/t) + E^(0.683013/t) *)

But I don't see an equivalent to SameTest for Plus

Jason B.
  • 68,381
  • 3
  • 139
  • 286