11

I need to draw some contour plots of very non-linear functions. As a simple example, take a Mandelbrot Set divergence contour near $z\approx i$. (Just to be clear, I'm not trying to write a Mandelbrot viewer, just picking a simple example of a recursive calculation).

z[n_, c_] := If[n > 0, z[n - 1, c]^2 + c, c];
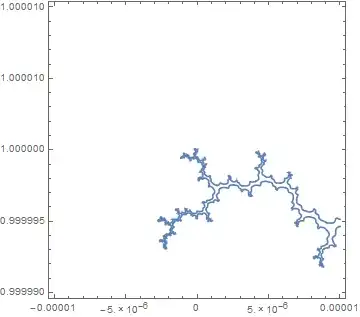
iter = 25;
ContourPlot[Abs[z[iter, x + I*y]] == 2, {x, -.00001, .00001}, {y, .99999, 1.00001}, 
   MaxRecursion -> 5]

MSetFilament

The higher we set iter, the higher we need to set MaxRecursion. But this slows the computation waaaay down, and I need to zoom in to smaller regions and display plots for higher values of iter.

However, we could avoid a lot of needless computation and make this calculation more efficient if we could somehow use our knowledge that:

  • If $z[r<n,c_0]>2$, then $c_0$ is outside the $z[n,c]==2$ contour, so there is no need to calculate the successive values $z[m>r,c_0]$.

  • The contours of successive values of iter are nested, i.e., the $z[n,c]==2$ contour is entirely inside or tangential to the $z[n-1,c]=2$ contour for all n.

I can think of ways to do this, but they involve having to write my own contour-plotting routine instead of using ContourPlot[]. Does anyone have a better idea than that?

m_goldberg
  • 107,779
  • 16
  • 103
  • 257
Jerry Guern
  • 4,602
  • 18
  • 47
  • Image processing? E.g., i = Import["https://29a.ch/mandelbrot/mandelbrot_small.png"]; ColorNegate@EdgeDetect@Binarize[ColorConvert[i, "Grayscale"], 0.3] -> http://i.stack.imgur.com/FR5v8.png – Michael E2 Jan 09 '16 at 01:11
  • @MichaelE2 I'm just using the M-Set here as example that's simpler than my actual recursive function, I'm not writing an M-Set viewer. :-) – Jerry Guern Jan 09 '16 at 01:13
  • My suggestion has nothing to do with writing an M-set viewer. It's about interpolating between values of the function, similar to a contour plot. Perhaps you mean something different by an "M-set viewer," but it's confusing to show a plot of a set and say you don't want to view it. (By the M-set, I'm assuming you don't mean the Mandelbrot set, but the contour for your own function(s).) – Michael E2 Jan 09 '16 at 01:54
  • @MichaelE2 I am completely confused by what you are telling me. Your comment above suggests Importing some mandelbrot png. I'm just asking how to make a faster contour plot of a really non-linear function. – Jerry Guern Jan 09 '16 at 02:01
  • The main point in my comment is about finding the contour in the array of function values (represented by the image data) with Binarize. There are efficient ways to generate images of the M-set. If there are such ways for your function, then I thought the approach might work for you. – Michael E2 Jan 09 '16 at 02:10
  • The first thing I'd try is to change your function to stop iterating as soon as $|z(r,c)|>2$. This doesn't change the contour, but now for most of the points in the plot range it won't have to iterate all the way to $n$. I don't know if it's easy to do this efficiently in a functional style; I would write an explicit loop instead. –  Jan 09 '16 at 04:34
  • @Rahul Right, that's what I was getting at when I said in the Question that I can think of ways to do this but I'd have to write my own contour plot routine instead of using ContourPlot[] – Jerry Guern Jan 09 '16 at 04:49
  • 1
    No, just change your definition of z to stop iterating sooner and use that in ContourPlot. –  Jan 09 '16 at 05:04

2 Answers2

13

Using NestWhile seems to work well

z[n_, c_] := NestWhile[(#^2 + c) &, c, Abs[#] <= 2 &, 1, n];
ContourPlot[Abs[z[iter, x + I*y]] == 2, {x, -.00001, .00001}, {y, .99999, 1.00001}, 
    MaxRecursion -> 5] // AbsoluteTiming

producing the plot in the question in about 10 seconds, as opposed to 180 seconds for the code in the question.

enter image description here

bbgodfrey
  • 61,439
  • 17
  • 89
  • 156
  • That's definitely an improvement from my z[n,c] function, and it does accomplish the first improvement I asked about, but when I zoom in its gets veeeery slow again, so I still wonder if that second improvement is possible. ContourPlot[ Abs[z[35, x + I*y]] == 2, {x, -.000001, .000001}, {y, .999999, 1.000001}, MaxRecursion -> 10] – Jerry Guern Jan 09 '16 at 05:37
  • ...or any other improvement anyone can think of. – Jerry Guern Jan 09 '16 at 05:44
  • 5
    @JerryGuern If you're looking for faster ways to code an iterative function, there are some ideas here: http://mathematica.stackexchange.com/questions/104/speeding-up-this-fractal-generating-code – Michael E2 Jan 09 '16 at 05:51
  • @JerryGuern When running the ContourPlot computation given in your comment above, Mathematica 10.3.0 quickly devours all the memory on my computer and then saturates disk transfer. If you are experiencing the same behavior, it would cause your computer to come to almost a halt. MaxRecursion is the issue. – bbgodfrey Jan 09 '16 at 10:45
  • 1
    @JerryGuern Continuing my last comment, MaxRecursion -> 5 required 14 sec, 6 required 78 sec, and 7 required longer than I cared to wait (at least 2000 sec). The reference provided by MichaelE2 suggests that plotting sometimes may take more time than computing z does, and I can easily believe that this is so. In any event, I do not believe that your second approach in the question will offer any significant savings over that obtained from the first approach. – bbgodfrey Jan 09 '16 at 11:39
3

Many years of Lisp and Scheme programming has given me a fondness for recursive functions. They don't have to have poor performance if some care is taken when writing them. For your problem I would write z as

z[n_, c0_] := z[n - 1, c0, c0^2 + c0]
z[0, _, c_] := c
z[n_, c0_, c_?(Abs[#] > 2 &)] := c
z[n_, c0_, c_] := z[n - 1, c0, c^2 + c0]

Note there is a cutoff for Abs[c] > 2. That gives a pretty good performance boost.

ContourPlot[Abs[z[25, x + I*y]] == 2, {x, -.00001, .00001}, {y, .99999, 1.00001}, 
  MaxRecursion -> 5] // AbsoluteTiming

test

Not as fast as bbgodfrey's NestWhile solution, but not too shabby.

m_goldberg
  • 107,779
  • 16
  • 103
  • 257