Histogram from relative frequency data;

Question

I've got a data set similar to the first and fourth column of this table http://mathworld.wolfram.com/FrequencyDistribution.html where the first column is the midpoint of a fixed range of values (although a solution with arbitrarily spaced segments would be great) and the second column is the corresponding relative frequency of that initial range of values being present.

 A = {{5, 0.0123445}, {15, 0.0342565}, {25, 0.0885784}, {35, 0.184694}, {45, 0.243735}, {55, 0.223433}, {65, 0.111512}, {75, 0.000000}, {85, 0.000000}, {95, 0.1014466}}

I want to plot a histogram/discrete probability distribution. I've found solutions to plotting histograms from pre-binned data https://stackoverflow.com/questions/15117024/histogram-with-frequency-data but this only works on integer values.

My probability data has ~6 significant digits and I would really prefer not to arbitrarily multiply my data by 10^6 to plot it then adjust the plot labels to divide by 10^6.

Am I trying to force a function to do something it's not designed to do, is there a better way of going about this?

Thanks!

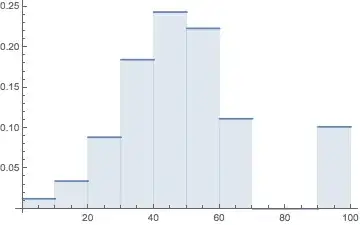
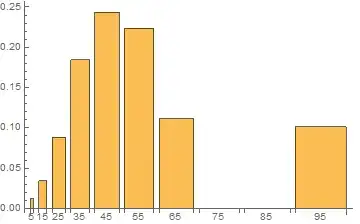
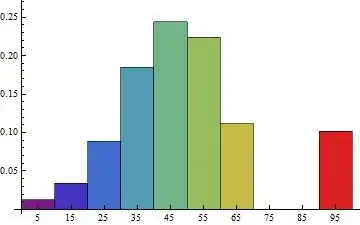
Maybe Histogram[a[[All, 2]], PlotRange -> {{0.00001, 1}, Automatic}] ? Where a is your data. — e.doroskevic, Jan 13 '16 at 00:14
@E.Doroskevic That attempt didn't work, when I tried to run that on my data the result was simply the y-axis. — Andrew Stewart, Jan 13 '16 at 00:52

eldo · Answer 1 · 2016-01-13T00:34:52.647

3

Maybe a simple BarChart with labels would suffice?

BarChart[list[[All, 2]], ChartLabels -> list[[All, 1]]]

Total@list[[All, 2]]

1.

Update

Unevenly spaced segments

list =
  {{5, 0.0123445}, {35, 0.0342565}, {45, 0.0885784}, {50, 0.184694},
   {52, 0.243735}, {55, 0.223433}, {65, 0.111512}, {75, 
    0.000000}, {85, 0.000000}, {95, 0.1014466}};

BarChart[list[[All, 2]], ChartLabels -> list[[All, 1]]]

edited Jan 13 '16 at 00:34

answered Jan 13 '16 at 00:13

eldo

67,911
5
60
168

Would this work with unevenly spaced segments? – Andrew Stewart Jan 13 '16 at 00:18
Yes, only the label numbers would change, see update of my answer – eldo Jan 13 '16 at 00:36
Thanks for the help, I'm not as familiar with the Charting functions. I would prefer to keep logical spacing on the 'x-axis' while simultaneously being able to set plotrange and independent plot markers etc.
(Using your methodology on my data yields this plot http://i.imgur.com/pJzIGnN.png which is great but not ideal, re: x-axis).
– Andrew Stewart Jan 13 '16 at 00:39

score 3 · Answer 2 · answered Jan 13 '16 at 00:50

3

You could simulate using EmpiricalDistribution. In the following I have changed A to a:

ed = EmpiricalDistribution[#2 -> #1 & @@ (Transpose@a)];
Histogram[RandomVariate[ed, 10000], Automatic, "Probability"]

answered Jan 13 '16 at 00:50

ubpdqn

60,617
3
59
148

Interesting, I think I might use this answer if an exact solution isn't possible. I bumped the 10000 to 10^7 and while it takes a few seconds to run it gives me relatively non-variable output. Thanks! – Andrew Stewart Jan 13 '16 at 01:05

Andy Ross · Accepted Answer · 2016-01-13T01:34:05.317

3

Alternatively, you could use WeightedData.

a = {{5, 0.0123445}, {15, 0.0342565}, {25, 0.0885784}, {35, 
   0.184694}, {45, 0.243735}, {55, 0.223433}, {65, 0.111512}, {75, 
   0.000000}, {85, 0.000000}, {95, 0.1014466}};

Histogram[WeightedData @@ Transpose[a], Length[a]]

You might also consider using DiscretePlot with an EmpiricalDistribution.

dist = EmpiricalDistribution[WeightedData @@ Transpose[a]]

DiscretePlot[PDF[dist, x], {x, a[[All, 1]]}, ExtentSize -> Full]

edited Jan 13 '16 at 01:34

answered Jan 13 '16 at 01:25

Andy Ross

19,320
2
61
93

Thanks! The DiscretePlot looks like it will work best. – Andrew Stewart Jan 13 '16 at 21:21

score 3 · Answer 4 · answered Jan 13 '16 at 14:36

If you are simply interested in plotting the data, you can use ListStepPlot:

ListStepPlot[A, "Center", Filling -> Axis, Joined -> False]

Notes

This will work with unevenly-spaced segments, since with the "Center" option, "the step extends to the center between neighboring points:"

B = {{5, 0.0123445}, {15, 0.0342565}, {22, 0.0885784}, {38, 0.184694}, {42, 0.243735}, 
     {55, 0.223433}, {65, 0.1115120}, {70, 0.0000000}, {85, 0.000000}, {95, 0.101447}};

ListStepPlot[B, "Center", Filling -> Axis, Joined -> False]

If you want to specify the right or left point instead, you can use the "Left" or "Right" options instead.

Since this is a plot, and not a chart, some of the nicer chart features are unavailable, and you will need to do more work to get the same result. For instance, if you want to be able to add labels (à la ChartLabels), you can use Labeled like so
```
C = Labeled[#, Chop@Round[Last@#, 0.001], Above] & /@ A;

ListStepPlot[C, "Center",
 Filling -> Axis,
 Joined -> False,
 ImagePadding -> {{Automatic, Automatic}, {Automatic, 10}},
 PlotMarkers -> "",
 PlotRangeClipping -> False]
```

score 1 · Answer 5 · answered Jan 13 '16 at 00:29

1

Similarl output to the above could be achieved using:

Code:

RectangleChart[a, ChartLabels -> a[[All, 1]], BarSpacing -> {10, 5}]

Output:

answered Jan 13 '16 at 00:29

e.doroskevic

5,959
1
13
32

Unfortunately, I think this suffers the same limitations of @eldo 's solution. Thanks for taking a look though. – Andrew Stewart Jan 13 '16 at 00:50

score 1 · Answer 6 · answered Aug 19 '17 at 04:59

1

You can use the data on frequencies as the third argument of Histogram:

{bincenters, frequencies} = Transpose[A];
spacing = First@Differences@bincenters;
bins = Append[bincenters - spacing/2, Last[bincenters] + spacing/2];

Histogram[{0}, {bins}, frequencies&, ChartStyle -> "Rainbow", 
 AspectRatio -> 1, Ticks -> {bincenters, Automatic}]

answered Aug 19 '17 at 04:59

kglr

394,356
18
477
896

Yes, this is the same kind of technique that I used in this answer: https://mathematica.stackexchange.com/questions/81155/how-to-create-a-bar-chart-from-a-list-of-heights-and-bin-delimiter-positions/151319#151319 – hftf Aug 19 '17 at 09:00

Histogram from relative frequency data;

6 Answers6

Notes

Linked