The ODE I need to solve is
$$\left(y^3y^{\prime\prime\prime}\right)^\prime+\frac{5}{8}xy^\prime-\frac{1}{2}y+\frac{c}{y}=0$$ where $\prime$ denotes differentiation, $c$ is a constant and $0<c\le1$. It needs 4 boundary conditions (BCs): $y^\prime(0)=y^{\prime\prime\prime}(0)=0$ are given, and the other two values of $y(0)$ and $y^{\prime\prime}(0)$ are determined by shooting for BCs at infinity (or $x_\text{Max}$).
Inspired by @ bbgodfrey's idea in this answer, I know that the far-field asymptotic behavior is given by DSolveing the remainder of the ODE after the nonlinear derivative term are neglected:
DSolve[5/8 x y'[x] - 1/2 y[x] + c/y[x] == 0, y[x], x]
Thus the far-field asymptotic behavior is $y= kx^{4/5}$, where $k$ is a constant. Accordingly, we refer to a solution with $y\sim x^{4/5}$ asymptotic behavior as a $x^{4/5}$ solution. Here, I want to search for this kind of solutions by shooting method in which the ODE is integrated from $x_0=0$ to some large value of $x_\text{Max}$, say $x_\text{Max}=10$.
The shooting parameters $y(0)$ and $y^{\prime\prime}(0)$ will be adjusted so that $y-\frac{5}{4}xy^\prime=0$ or $y+\frac{25}{4}x^2y^{\prime\prime}=0$ at $x=x_\text{Max}$ is satisfied. The two BCs were chosen to be independent to involve low-order derivatives and to require $y\propto x^{4/5}$ at the end of the integration interval.
Thanks to @ xzczd's answer to this question, an example of the code is:
c = 1;
(*c=1/10;*)
ode = D[y[x]^3*y'''[x], x] + 5/8 x y'[x] - 1/2 y[x] + c/y[x] == 0;
bc1 = y[x] - 5/4 x y'[x] == 0;
bc2 = y[x] + 25/4 x^2 y''[x] == 0;
Thank again to this answer, I can obtain the series solution at $x_0=0$ with seriesDSolve
solSeries = seriesDSolve[ode, y, {x, 0, 5},
{y[0] -> a, y'[0] -> 0, y''[0] -> b, y'''[0] -> 0}]
We thus obtain a set of boundary conditions at $x=x_0$ by
newbclist = Thread[(Derivative[#][y][x0] ==
(D[Normal@solSeries, {x, #}] /. x -> x0) &) /@ Range[0, 3]]
Then, give the interval, solve the ODE and plot the parameter plane
x0 = 0; xMax = 6;
sol = ParametricNDSolveValue[{ode, newbclist}, y, {x, x0, xMax}, {a, b}]
ContourPlot[{bc1, bc2} /. x -> xMax /. y -> sol[a, b] // Evaluate,
{a, 0.2, 0.6}, {b, -0.05, 1}]
Unfortunately, Mathematica gives something like this:
ParametricNDSolveValue::ndsz: At x$803007 == 0.27144285125721357`, step size is effectively zero; singularity or stiff system suspected.
as encounters in this problem.
After some experiments, I found the situation appears to be worse for a larger parameter $c$, i.e. $c\rightarrow 1$. And I also played with the intervals of $a$ and $b$ but it seems no help. Three ugly results for your reference (sorry!...)
1. When I use c = 1/10, xMax = 0.5 with {a, -0.2, 1}, {b, -0.1, 1}, ContourPlot gives
2. When I use c = 1/10, xMax = 0.5 with {a, 0.2, 0.6}, {b, -0.05, 1}, ContourPlot gives
3. When I change to bc1 = 1/2 y[x] - 5/8 x y'[x] - c/y[x] == 0; with c = 1, xMax = 6 and {a, -0.2, 1}, {b, -0.1, 1}, ContourPlot gives
To sum up, my questions are:
(1) After I find the parameter $y(0)$ and $y^{\prime\prime}(0)$, how can I figure out the associated constant $k$ in the far-field asymptotic behavior $y= kx^{4/5}$?
(2) Is it possible to estimate the parameters $y(0)$ and $y^{\prime\prime}(0)$ automatically to start the integration, as shown in this answer?
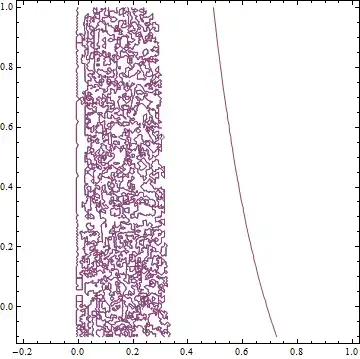

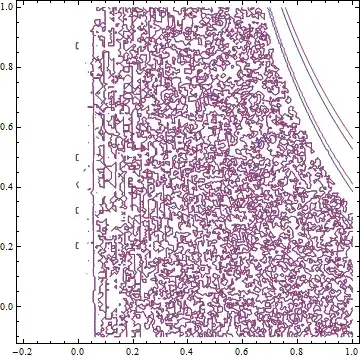

{a, b}can't lead to a solution extending to infinity. Just observe this:mid = sol[0.6, 0.6]; {{lb, rb}} = mid["Domain"]; Plot[mid[t], {t, lb, rb}, PlotRange -> All]– xzczd Jan 16 '16 at 04:29