4

I am working with some students on transforming conic sections by rotation of axes. I would like to create a simple Manipulate where I plot the before and after graph, and then use a Slider to rotate the original graph until it matches the final graph, and then confirm that the angle we used for the transformation worked.

For example, in the command below, we have an original ellipse with an x y term, that, when transformed to eliminate the x y term, gives an ellipse with a vertical major axis. (the "same" ellipse, rotated)

I'd like to add a Slider that would allow me to rotate the original ellipse until it matches the transformed ellipse. I tried using Rotate, but must not be using the right syntax. I know I am trying to combine graphics "objects" and it would help to see how to do that in the right way.

 ContourPlot[{8 x^2 + 4 x y + 5 y^2 == 9, 
  45 x^2 + 20 y^2 == 45} , {x, -2, 2}, {y, -2, 2}, Frame -> False]

Any help would be appreciated.

Kuba
  • 136,707
  • 13
  • 279
  • 740
Tom De Vries
  • 3,758
  • 18
  • 36
  • 1
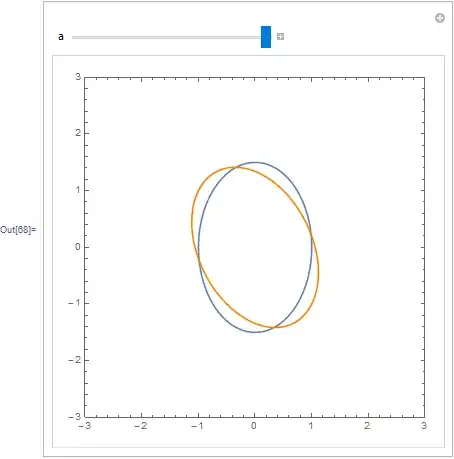
    f[{x_, y_}] := 8 x^2 + 4 x y + 5 y^2 - 9; Manipulate[ ContourPlot[{f[{x, y}] == 0, f[RotationTransform[p][{x, y}]]}, {x, -2, 2}, {y, -2, 2}, Frame -> False,PlotLabel -> f[RotationTransform[p][{x, y}]]], {p, 0, 2 Pi}] – Dr. belisarius Jan 19 '16 at 22:02

1 Answers1

8

If you leave ContourPlot outside you can get quite nice performance:

static = ContourPlot[45 x^2 + 20 y^2 == 45, {x, -2, 2}, {y, -2, 2},
   Frame -> False];
dynamic = ContourPlot[8 x^2 + 4 x y + 5 y^2 == 9, {x, -2, 2}, {y, -2, 2}, 
   Frame -> False, ContourStyle -> Orange];

Manipulate[
 Graphics[{       
   First@static,       
   Dynamic[Rotate[First@dynamic, a]]
   },
   PlotRange -> 3, Frame -> True],
 {a, 0, 2 Pi}
 ]

enter image description here

Kuba
  • 136,707
  • 13
  • 279
  • 740
  • I see that the structure of the graphics is accessed using the First of a graphics object. That helped a lot and I will certainly use that in the future. I think Dr. belisarius' answer is really helpful to see things in real time, as the equation changes, but I will confess I don't understand the structure there at all, which is often the case for me! As always, answers are given so freely and so quickly, this site is an amazing resource! Thank you! – Tom De Vries Jan 20 '16 at 11:56
  • @TomDeVries problem with contour plot is that it samples the whole domain looking for a contour. If you switch to the parametric representation then you can use ParametricPlot which should be faster because it only draws a line where it should be. So then you can use it in Manipulate and dynamically adjust parameters too. – Kuba Jan 20 '16 at 12:01