2

I have an experimental data from Michelson interference and I can fit the envelope in OriginPro9.0 using Global Fitting with shared parameters. The figure by OriginPro9.0 is like this:enter image description here

However, I hope to realize this function in Mathematica. Here is what I did in Mathematica:

The source data is here.

Firstly, I smooth the up envelop and down envelop. 

SetDirectory[NotebookDirectory[]];
name = "MichelsonInterference.txt";
b = Import[name, "Table"];
xmin = Min[b[[All, 1]]]; xmax = Max[b[[All, 1]]]; ymin = Min[b[[All, 2]]]; ymax = Max[b[[All, 2]]];
wd = 3; (*window width for average*) 
step = 3;(*scan step in x, from xmin to xmax with the step*) 
windowMin[data_, w_][pt_] := {pt, Min[Cases[data, {x_, y_} /; pt - w <= x <= pt + w][[All, 2]]]}
windowMax[data_, w_][pt_] := {pt, Max[Cases[data, {x_, y_} /; pt - w <= x <= pt + w][[All, 2]]]}
upenv = Table[windowMax[b, wd][t], {t, xmin, xmax, step}];
downenv = Table[windowMin[b, wd][t], {t, xmin, xmax, step}];
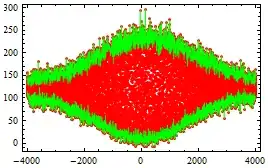
fig1 = ListLinePlot[b, PlotRange -> All, PlotStyle -> {Red}, Joined -> False, Frame -> True, Axes -> False];
fig2 = ListLinePlot[{upenv, downenv}, PlotRange -> All, Axes -> False,  Frame -> True, PlotStyle -> {{Green, Thin}, {Green, Thin}}];
Show[fig1, fig2]

The result is here:

enter image description here

Secondly, I try to fit the up envelop and down envelop with the same parameters {y0, xc, w}, but different A, using the method introduced here.

data1 = upenv;
data2 = downenv;
Remove[f, y0, A, w, xc];
f[x_, A_, y0_, xc_, w_] := y0 + A/(w Sqrt[π/2])*Exp[-2*((x - xc)/w)^2]; 
x0 = (xmin + xmax)/2; h = ymax; Δx = (xmax - xmin)/4;
vars = {{y0, 0}, {xc, x0}, {w, Δx/2}, {A1, h*Δx/2}, {A2, -h*Δx/2}};
logModel = -Total[(data1[[All, 2]] - (f[#, A1, y0, xc, w] & /@ 
    data1[[All, 1]]))^2]/2 - Total[(data2[[All, 2]] - (f[#, A2, y0, xc, w] & /@ data2[[All, 1]]))^2]/2;
fit = FindMaximum[logModel, vars]

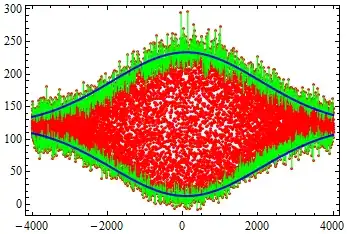
The result is enter image description here

With these fitted values, I plot all the figures together.

Show[ListLinePlot[b, PlotRange -> All, Joined -> False, PlotStyle -> {Red, Thin}],  ListLinePlot[{upenv, downenv}, PlotRange -> All, Axes -> False, Frame -> True, PlotStyle -> {{Green, Thin}, {Green, Thin}}],        Plot[  121.6 + 551180/(3927.6 Sqrt[π/2])*Exp[-2*((x - 95.64)/ 3927.6 )^2], {x, xmin, xmax}, PlotStyle -> {Blue, Thick}, PlotRange -> All], Plot[121.6 + -537445/(3927.6 Sqrt[π/2])* Exp[-2*((x - 95.64)/ 3927.6 )^2], {x, xmin, xmax}, PlotStyle -> {Blue, Thick}, PlotRange -> All],Axes -> False, Frame -> True, AspectRatio -> .67, LabelStyle -> Directive[Black, Medium], ImageSize -> {300, 200}]

The final result by Mathematica is

enter image description here

My problem is that this fitted figure by Mathematica is different from the one by OriginPro9.0 (the first figure). I hope to obtain the same result as what I got in OriginPro9.0. For example, the FWHM of figure by Mathematica should be narrower. Could you help me by improving my Mathematica codes? Thank you all in advance!

Community
  • 1
user14634
  • 771
  • 6
  • 17
  • Can you provide the method/path that led to the Origin fit? Reverse-engineering on our side seems ... inefficient. – Yves Klett Jan 20 '16 at 07:38
  • 1
    Looking on your data (Red and Green), I see that the first and the last figures are different. The green stripes are coinciding at the edges at the first figure and don't coincide at the last one.. And the blue curves has the same behavior : one is coinciding relatively far from edges and the second does not coincide at all.

    It seems that approx. in Origin was done for unfiltered data..

     – Rom38 Jan 20 '16 at 07:46
  • @Yves Klett, In Origin Pro, (Origin withou Pro does not have this function) we need two step to obtain the result. The first step is envelop fit to extract the up envelope and down envelope. Using "Envelop" (Analysis -> Signal Processing -> Envelop) .The second step is to fit the up envelope and down envelope. Choose Nonliear curve fitting-->gauss, then data selection.->Input Data ->Multi-Data Fit Mode -> Global Fit; share fitting parameters (y0, xc, w). – user14634 Jan 20 '16 at 07:49

0 Answers0